题目内容

已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两个顶点为A1（-a，0），A2（a，0），与y轴平行的直线交椭圆于P1、P2，求A1P1与A2P2交点的轨迹方程．
考点：轨迹方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：设P1（x，y），则P2（x，-y），由椭圆的参数方程，分别求出A1P1的方程和A2P2的方程（含参数θ），联立方程后，消去参数θ即可得到满足条件的曲线方程．
解答： 解：设P1（x，y），则P2（x，-y）
P1，P2在椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上，则x=asinθ，y=bcosθ
则A1P1的方程为
-a-x
0-y
=
asinθ+a
bcosθ
①
A2P2的方程为
a-x
0-y
=
-asinθ+a
bcosθ
②
联立方程①，②得x=acscθ，y=bcotθ
消去θ可得A1P1与A2P2交点的轨迹方程
x2
a2
-
y2
b2
=1．
点评：本题考查的知识点是轨迹方程，椭圆的简单性质，其中根据椭圆的参数方程，求出A1P1的方程和A2P2的方程，进而求出两条直线交点的坐标，是解答本题的关键．
练习册系列答案
相关题目
已知函数f（x）=
2x2-3x+1，x≤1
-x2+x，x＞1
，关于x的方程f（x）=m（m∈R）恰有三个互不相等的实数根x1，x2，x3，则x1+x2+x3的取值范围是（　　）
A、（
3
4
，
8-
6
4
）
B、（
5
2
，
8+
6
4
）
C、（1，
2+
6
4
）
D、（
5
2
，
11+
6
4
）
设函数f（x）=ex（sinx-1）
（Ⅰ）求函数f（x）的单调增区间；
（Ⅱ）当x∈[-
3
4
π，
3
4
π]时，求函数的最大值和最小值．
某大型公益活动从一所名牌大学的四个学院中选出了18名学生作为志愿者，参加相关的活动事宜．学生来源人数如下表：
学院外语学院生命科学学院化工学院艺术学院
人数4635
（Ⅰ）若从这18名学生中随机选出两名，求两名学生来自同一学院的概率；
（Ⅱ）现要从这18名学生中随机选出两名学生向观众宣讲此次公益活动的主题．设其中来自外语学院的人数为ξ，令η=2ξ+1，求随机变量η的分布列及数学期望E（η）．
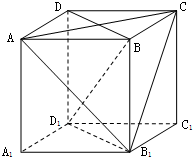如图，正方体ABCD-A1B1C1D1是棱长为1的正方体．
（1）求证：BD1⊥平面ACB1；
（2）求三棱锥B-ACB1的体积．
已知函数f（x）=
x
1+x
（x＞0），数列{an}满足：a1=
1
2
，an+1=f（an）（n∈N*）
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）令函数g（x）=f（x）（1+x）2，数列{cn}满足：c1=
1
2
，cn+1=g（cn）（n∈N+），求证：对于一切n≥2的正整数，都满足：1＜
1
1+c1
+
1
1+c2
+…+
1
1+cn
＜2．
已知等比数列{an}的首项a1=2013，公比q=-
1
2
，数列{an}前n项和记为Sn，前n项积记为Tn．
（1）证明：S2≤Sn≤S1；
（2）求n为何值时，Tn取得最大值；
（3）证明：若数列{an}中的任意相邻三项按从小到大排列，则总可以使其成等差数列；若所有这些等差数列的公差按从小到大的顺序依次记为d1，d2，…，dn，则数列{dn}为等比数列．
设f（x）=
2x+4
4x+8
，求证：对任意实数a，b，不等式f（a）＜b2-3b+
21
4
恒成立．
人民日报3月14日报道，中国人民银行已下发通知，要求暂停二维码（条码）支付，虚拟信用卡等支付业务和产品．前不久，某调研机构调研了在校大学生网上购物的情况，随机调查了16位在校大学生的网购比例，结果如茎叶图所示（图中茎7叶3表示73%，其余相同）：
（Ⅰ）求从这16个在校大学生随机选取3个，至多有1个网购比例不低于95%的概率；
（Ⅱ）以这16个在校大学生的样本数据来估计全国的总体数据，若从全国任选3位大学生，记ξ表示抽到网购比例不低于95%的人数，求ξ的分布列及数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网