题目内容
7.求证:$\frac{2sin(θ-\frac{3π}{2})cos(θ+\frac{π}{2})-1}{1-2co{s}^{2}(θ+\frac{3}{2}π)}$=$\frac{tan(9π+θ)+1}{tan(π+θ)-1}$.分析 利用诱导公式,同角三角函数基本关系式化简证明左边=$\frac{tanθ+1}{tanθ-1}$=右边,即可得证.
解答 证明:∵左边=$\frac{2sin(θ-\frac{3π}{2})cos(θ+\frac{π}{2})-1}{1-2co{s}^{2}(θ+\frac{3}{2}π)}$=$\frac{-2cosθsinθ-1}{cos2θ}$=-$\frac{sin2θ+1}{cos2θ}$=-$\frac{\frac{2tanθ}{1+ta{n}^{2}θ}+1}{\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}}$=$\frac{(1+tanθ)^{2}}{(tanθ+1)(tanθ-1)}$=$\frac{tanθ+1}{tanθ-1}$,
右边=$\frac{tan(9π+θ)+1}{tan(π+θ)-1}$=$\frac{tanθ+1}{tanθ-1}$.
∴左边=右边,得证.
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数的化简求值中的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.曲线y=$\sqrt{x}$在(1,1)处的切线与直线2ax-y-6=0平行,则a=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
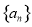 的前
的前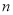 项和为
项和为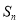 ,且满足
,且满足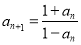 ,若
,若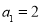 ,则
,则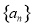 的前2017项的积为( )
的前2017项的积为( )