题目内容
12.已知△ABC三内角的正弦值等于△A1B1C1的三内角的余弦值,角A、B、C所对应的边为a,b,c,且A为钝角,a=2$\sqrt{5}$.b=2$\sqrt{2}$,则△ABC的面积为2.分析 设:sinA=cosA1,sinB=cosB1,sinC=cosC1,可得A1,B1,C1 都为锐角,又A为钝角,则B,C为锐角,结合诱导公式及三角形内角和定理可知:A=A1=A-90°,B1=90°-B,C1=90°-C,
相加可解得A=$\frac{3π}{4}$,利用余弦定理可得c2+4c-12=0,解得c,利用三角形面积公式即可得解.
解答 解:∵△ABC三内角的正弦值等于△A1B1C1的三内角的余弦值,
∴不妨设:sinA=cosA1,sinB=cosB1,sinC=cosC1,
∵cosA1>0,cosB1>0,cosC1>0,
∴A1,B1,C1 都为锐角,
又A为钝角,则B,C为锐角,结合诱导公式及三角形内角和定理可知:A=A1=A-90°,B1=90°-B,C1=90°-C,
相加可得:A-B-C+90°=A1+B1+C1,
解得:A=$\frac{3π}{4}$.
由余弦定理a2=b2+c2-2bccosA,可得:20=8+c2+4c,即:c2+4c-12=0,解得:c=2,
∴S△ABC=$\frac{1}{2}$bcsinA=2.
故答案为:2.
点评 本题主要考查了三角函数恒等变换的应用,考查了余弦定理,三角形面积公式在解三角形中的应用,考查了转化思想,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
17.下列求导数运算正确的是( )
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{x^{2}}$ | B. | (log2x)′=$\frac{1}{xln2}$ | C. | (3x)′=3xlog3e | D. | (x2)′=-2x |
1.函数y=sin2x的图象在点A($\frac{π}{6}$,$\frac{1}{4}$)处的切线的斜率是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
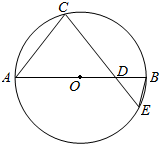 如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=2$\sqrt{2}$,BD=2.
如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=2$\sqrt{2}$,BD=2. ,则
,则 为( )
为( ) B.
B.
 D.
D.