题目内容
16.已知函数f(x)=ex(-x2+b).(1)若函数f(x)在点P(0,f(0))处的切线方程为y=3x+3,求函数f(x)的表达式;
(2)求函数f(x)的单凋区间与极值点.
分析 (1)f′(x)=ex(-x2-2x+b).由点P(0,f(0))处的切线方程为y=3x+3.可得f(0)=3,f′(0)=3.解得b,可得函数f(x)的表达式;
(2)由f′(x)<0,f′(x)>0解出可得函数f(x)的单调递减、增区间,即可求出极值点.
解答 解:(1)f′(x)=ex(-x2-2x+b).
∵点P(0,f(0))处的切线方程为y=3x+3.
∴f(0)=3,f′(0)=3.
∴b=3,
∴f(x)=ex(-x2+3).
(2)f′(x)=ex(-x2-2x+3)=-ex(x+3)(x-1),
由f′(x)<0,化为(x+3)(x-1)>0,解得x>1或x<-3,
∴函数f(x)的单调递减区间为(-∞,-3),(1,+∞);单调递增区间是(-3,1)
∴极值点为-3,1.
点评 本题考查了利用导数研究其单调性、极值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.函数y=sin2x的图象在点A($\frac{π}{6}$,$\frac{1}{4}$)处的切线的斜率是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
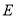 的方程为
的方程为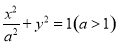 ,
, 为坐标原点,直线
为坐标原点,直线 与椭圆
与椭圆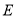 交于点
交于点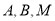 为线段
为线段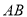 的中点.
的中点.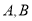 分别为
分别为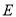 的左顶点和上顶点,且
的左顶点和上顶点,且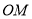 的斜率为
的斜率为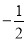 ,求
,求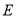 的标准方程;
的标准方程;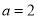 ,且
,且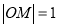 ,求
,求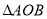 面积的最大值.
面积的最大值.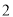 的等边
的等边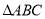 的边角地,现修成草坪,图中
的边角地,现修成草坪,图中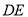 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在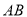 上,
上,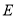 在
在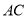 上.
上.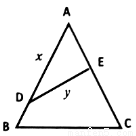
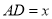 (
(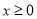 ),
), ,求用
,求用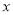 表示
表示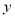 的函数关系式;
的函数关系式;