题目内容
7.设函数f(x)=2$\sqrt{3}$sinxcosx-sin2x+cos2x.(1)求f(x)的最小正周期及单调递增区间;
(2)若g(x)=f(x)-m在x∈[0,$\frac{π}{2}$]上有两个不同的零点,求实数m的取值范围.
分析 (1)利用倍角公式可得:函数f(x)=2sin(2x+$\frac{π}{6}$),再利用三角函数的周期性与单调性即可得出;
(2)分别画出y=f(x)和y=m的图象,由图象可知,1≤m<2.
解答 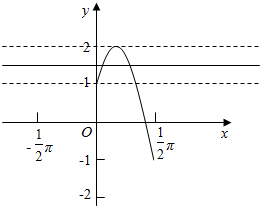 解:(1)f(x)=2$\sqrt{3}$sinxcosx-sin2x+cos2x=$\sqrt{3}$sin2x+cos2x=2($\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x)=2sin(2x+$\frac{π}{6}$),
解:(1)f(x)=2$\sqrt{3}$sinxcosx-sin2x+cos2x=$\sqrt{3}$sin2x+cos2x=2($\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x)=2sin(2x+$\frac{π}{6}$),
∴T=$\frac{2π}{2}$=π,-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,
∴-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,
∴f(x)的单调递增区间为[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z,
(2)g(x)=f(x)-m在x∈[0,$\frac{π}{2}$]上有两个不同的零点,
∴f(x)-m=0,
即f(x)=m,
分别画出y=f(x)和y=m的图象,如图所示:
由图象可知,当1≤m<2时,y=f(x)和y=m有两个交点,
∴g(x)=f(x)-m在x∈[0,$\frac{π}{2}$]上有两个不同的零点,m的范围为[1,2).
点评 本题考查了倍角公式、三角函数的周期性与单调性,函数的零点的判定方法,体现了数形结合及转化的数学思想,画出图形是解题的关键,属于中档题

练习册系列答案
相关题目
12.函数y=$\frac{2}{x}$-lnx的零点所在区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
19.已知函数f(x)=(x-1)3+2014(x-1),等差数列{an}的前n项和为Sn,且f(a2)+f(a2014)=0,则S2015=( )
| A. | 4030 | B. | 4028 | C. | 2015 | D. | 2014 |
12.△ABC中,点D在BC上,AD平分∠BAC,若$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AC}=\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,则$\overrightarrow{AD}$=( )
| A. | $\frac{2}{5}\overrightarrow{a}+\frac{3}{5}\overrightarrow{b}$ | B. | $\frac{4}{5}\overrightarrow{a}+\frac{3}{5}\overrightarrow{b}$ | C. | $\frac{3}{5}\overrightarrow{a}+\frac{4}{5}\overrightarrow{b}$ | D. | $\frac{3}{5}\overrightarrow{a}+\frac{2}{5}\overrightarrow{b}$ |