题目内容
8.已知抛物线C:y2=-4x.(Ⅰ)已知点M在抛物线C上,它与焦点的距离等于5,求点M的坐标;
(Ⅱ)直线l过定点P(1,2),斜率为k,当k为何值时,直线l与抛物线:只有一个公共点;两个公共点;没有公共点.
分析 (Ⅰ)已知点M在抛物线C上,它与焦点的距离等于5,利用抛物线的定义,建立方程,即可求点M的坐标;
(Ⅱ)由方程组$\left\{{\begin{array}{l}{y=kx-k+2}\\{{y^2}=-4x}\end{array}}\right.$可得:ky2+4y+4k-8=0,利用判别式,即可得出结论.
解答 解:(Ⅰ)点M在抛物线C上,设$C(-\frac{y^2}{4},y)$,设焦点为F,$|CF|=|-\frac{y^2}{4}|+1=5$---(2分)
解得:y2=16,故点M(-4,4)或M(-4,-4)----------------------------(4分)
(Ⅱ)由题意设直线l的方程:y=kx-k+2
由方程组$\left\{{\begin{array}{l}{y=kx-k+2}\\{{y^2}=-4x}\end{array}}\right.$可得:ky2+4y+4k-8=0---(1)----------(5分)
(1)当k=0时,由(1)得y=2带入y2=-4x,x=-1,
此时直线与抛物线只有一个公共点.---------------------------------------------------------(6分)
(2)当k≠0时,(1)的判别式△=16-4k(4k-8)=-16(k2-2k-1)-------(7分)
当△=0时,$k=1+\sqrt{2}$或$k=1-\sqrt{2}$,此时直线与抛物线只有一个公共点;------(8分)
当△>0时,$1-\sqrt{2}<k<1+\sqrt{2}$,此时直线与抛物线有两个公共点;-----------(10分)
当△<0时,$k>1+\sqrt{2}$或$k<1-\sqrt{2}$,此时直线与抛物线没有公共点.-----------(12分)
点评 本题考查抛物线的方程与定义,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | (0,$\frac{1}{e}$] | B. | (一∞,$\frac{1}{e}$] | C. | (0,$\frac{1}{e}$) | D. | (一∞,$\frac{1}{e}$) |
| A. | 1 | B. | 9 | C. | 17 | D. | 19 |
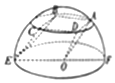 如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )
如图所示,三棱柱OAD-EBC,其中A,C,B,D,E均为以O为球心,半径为4的半球面上,EF为直径,侧面ABCD为边长等于4的正方形,则三棱柱OAD-EBC的高为( )| A. | $\frac{8\sqrt{6}}{3}$ | B. | $\frac{4\sqrt{6}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |