题目内容
3.直线$\frac{x}{3}$-$\frac{y}{4}$=1在x轴上的截距是( )| A. | -3 | B. | 3 | C. | -4 | D. | 4 |
分析 令y=0即可求得答案.
解答 解:令y=0,则x=3.即直线$\frac{x}{3}$-$\frac{y}{4}$=1在x轴上的截距是3.
故选:B.
点评 本题考查直线的截距式方程,是一道基础题.

练习册系列答案
相关题目
18.复数$\frac{5}{-2+i}$在复平面上的对应点的坐标是( )
| A. | (2,1) | B. | (-2,1) | C. | (-2,-1) | D. | (2,-1) |
15. 已知函数f(x)的定义域为[-2,6],x与f(x)部分对应值如表,f(x)的导函数y=f(x)的图象如图所示.
已知函数f(x)的定义域为[-2,6],x与f(x)部分对应值如表,f(x)的导函数y=f(x)的图象如图所示.
下列结论:
①函数f(x)在(0,3)上是增函数;
②曲线y=f(x)在x=4处的切线可能与y轴垂直;
③如果当x∈[-2,t]时,f(x)的最小值是-2,那么t的最大值为5;
④?x1,x2∈[-2,6],都有|f(x1)-f(x2)|≤a恒成立,则实数a的最小值是5,其中正确结论的个数是( )
 已知函数f(x)的定义域为[-2,6],x与f(x)部分对应值如表,f(x)的导函数y=f(x)的图象如图所示.
已知函数f(x)的定义域为[-2,6],x与f(x)部分对应值如表,f(x)的导函数y=f(x)的图象如图所示.| x | -2 | 0 | 5 | 6 |
| f(x) | 3 | -2 | -2 | 3 |
①函数f(x)在(0,3)上是增函数;
②曲线y=f(x)在x=4处的切线可能与y轴垂直;
③如果当x∈[-2,t]时,f(x)的最小值是-2,那么t的最大值为5;
④?x1,x2∈[-2,6],都有|f(x1)-f(x2)|≤a恒成立,则实数a的最小值是5,其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.已知角α的终边在直线y=$\frac{4}{3}$x上,则cosα-sinα的值等于( )
| A. | $\frac{4}{3}$ | B. | -$\frac{1}{5}$或$\frac{1}{5}$ | C. | -$\frac{3}{4}$或$\frac{3}{4}$ | D. | $\frac{1}{5}$ |
9.在△ABC中,AB=2,AC=3,A=60°,则BC=( )
| A. | $\sqrt{6}$ | B. | $\sqrt{7}$ | C. | $\sqrt{19}$ | D. | 2$\sqrt{5}$ |
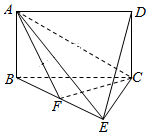 如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.
如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.