题目内容
15.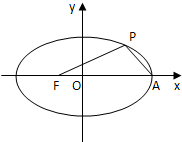 如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F、A分别是椭圆的一个焦点和顶点,P是椭圆上任意一点,则$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值为4.
如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F、A分别是椭圆的一个焦点和顶点,P是椭圆上任意一点,则$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值为4.
分析 利用椭圆的离心率求出c,推出b,求解椭圆的方程,推出F,A,设出P的坐标,利用向量的数量积化简求解最值即可.
解答 解:焦点在x轴上的椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,可得a=2,c=1,则b=$\sqrt{3}$,
椭圆方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
则F(-1,0),A(2,0),设P(2cosθ,$\sqrt{3}sinθ$),
则$\overrightarrow{PF}$=(-1-2cosθ,-$\sqrt{3}$sinθ),$\overrightarrow{PA}$=(2-2cosθ,-$\sqrt{3}$sinθ),
则$\overrightarrow{PF}$•$\overrightarrow{PA}$=(-1-2cosθ,-$\sqrt{3}$sinθ)(2-2cosθ,-$\sqrt{3}$sinθ)=cos2θ-2cosθ+1
=(cosθ-1)2,
当cosθ=-1时,上式取得最大值为4.
故答案为:4.
点评 本题考查椭圆的简单性质的应用,直线与椭圆的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
8.设集合A={x|$\frac{x-2}{x+3}$≤0},B={x|-4≤x≤1},则A∩B=( )
| A. | [-3,1] | B. | [-4,2] | C. | [-2,1] | D. | (-3,1] |
7.从标有1、2、3、4的卡片中不放回地先后抽出两张卡片,则4号卡片“第一次被抽到的概率”、“第二次被抽到的概率”、“在整个抽样过程中被抽到的概率”分别是( )
| A. | $\frac{1}{4},\frac{1}{4},\frac{1}{2}$ | B. | $\frac{1}{4},\frac{1}{4},\frac{1}{4}$ | C. | $\frac{1}{3},\frac{1}{3},\frac{1}{2}$ | D. | $\frac{1}{4},\frac{1}{3},\frac{1}{2}$ |
4.把A,B,C,D 4张纸牌随机地分发给甲,乙,丙,丁四个人,每人一张,则事件“乙分得A牌”与事件“丁分得A牌”是( )
| A. | 不可能事件 | B. | 互斥但不对立事件 | ||
| C. | 对立事件 | D. | 以上答案都不对 |
 如图,四棱锥P-ABCD中,AD⊥平面PAB,AP⊥AB.
如图,四棱锥P-ABCD中,AD⊥平面PAB,AP⊥AB.



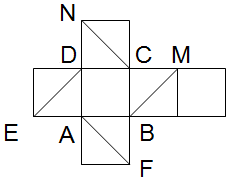 如图是正方体的平面展开图,则下列结论中正确的有(3)(4).
如图是正方体的平面展开图,则下列结论中正确的有(3)(4).