题目内容
8.下列命题中正确的是( )| A. | 若α>β,则sinα>sinβ | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 已知函数f(x)=x3+ax2+bx+c,若f(x)在区间(-1,0)上单调递减,则a2+b2的取值范围为$[{\frac{9}{5},+∞})$ | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
分析 在A中,举出反例即可;在B中,全称命题的否定是特称命题;在C中,f′(x)=3x2+2ax+b,由函数单调性质得到f′(x)≤0在(-1,0)上恒成立,由线性规划能求出a2+b2的取值范围;在D中,“若xy=0,则x=0或y=0”的逆否命题为“若x≠0且y≠0,则xy≠0”.
解答 解:在A中,由361°>30°,则sin361°<sin30°,故A错误;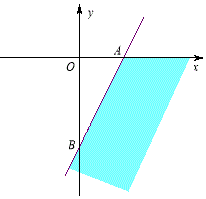
在B中,全称命题的否定是特称命题,所以命题:“?x>1,x2>1”的否定是“?x>1,x2≤1”,故B错误;
在C中,f′(x)=3x2+2ax+b,
∵f(x)在区间(-1,0)上单调递减,∴f′(x)≤0在(-1,0)上恒成立,
∴f′(-1)≤0且f′(0))≤0,即3-2a+b≤0且b≤0,
由线性规划知,a2+b2的几何意义是可行域内的点到(0,0)点的距离的平方,如图,
点(a,b)在直线3-2x+y=0的右下方及x轴下方(如图),
点(a,b)到原点的距离最小值为$\frac{3}{\sqrt{(-2)^{2}+{1}^{2}}}$=$\frac{3}{\sqrt{5}}$,无最大值,故a2+b2的取值范围为$[{\frac{9}{5},+∞})$,故C正确;
在D中,“若xy=0,则x=0或y=0”的逆否命题为“若x≠0且y≠0,则xy≠0”,故D错误.
故选:C.
点评 本题考查命题的真假判断,涉及正弦函数、全称命题、导数、线性规划、复合命题等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、函数与方程思想、化归与转化思想,是中档题.

练习册系列答案
相关题目
18.某程序框图如图所示,若t=7,则输出的值为( )
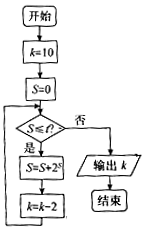

| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
19.已知$\overrightarrow{a},\overrightarrow{b}$均为单位向量,它们的夹角为60°,那么$\overrightarrow{a}•\overrightarrow{b}$=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
3.将函数$f(x)=2cos(\frac{x}{2}-\frac{π}{6})$的图象向左平移$\frac{π}{3}$单位后得到函数g(x)的图象,则函数g(x)在[-π,4π]上的图象与直线y=1的交点的横坐标之和为( )
| A. | 2π | B. | 3π | C. | $\frac{10π}{3}$ | D. | $\frac{11π}{3}$ |
20.已知函数f(x)=sin(ωx+φ)$(ω>0,|φ|<\frac{π}{2})$,其图象相邻两对称轴之间的距离为$\frac{π}{2}$,且函数$f(x+\frac{π}{12})$是偶函数,则下列结论正确的是( )
| A. | f(x)在$[{\frac{3π}{4},π}]$上单调递增 | B. | f(x)的最小正周期为2π | ||
| C. | f(x)的图象关于点$(\frac{7π}{12},0)$对称 | D. | f(x)的图象关于直线$x=-\frac{7π}{12}$对称 |
12.数集P={x|x=(2n+1)π,n∈Z}与数集Q={x|x=(4m±1)π,m∈Z}之间的关系是( )
| A. | P⊆Q | B. | P=Q | C. | Q⊆P | D. | P≠Q |