题目内容
抛物线y=
x2的焦点坐标为（ ）
| 1 |
| 8 |
A、（0，
| ||
B、（
| ||
| C、（0，4） | ||
| D、（0，2） |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：把抛物线的方程化为标准形式，即可得出结论．
解答：
解：把抛物线y=
x2方程化为标准形式为x2=8y，
∴焦点坐标为（0，2）．
故选：D．
| 1 |
| 8 |
∴焦点坐标为（0，2）．
故选：D．
点评：本题考查抛物线的标准方程和简单性质的应用，把抛物线的方程化为标准形式是关键．
练习册系列答案
相关题目
执行如图所示的程序框图，如果输入a=2，那么输出的a值为（ ）
| A、4 |
| B、16 |
| C、256 |
| D、log316 |
已知双曲线
-
=1的左、右焦点为F1，F2，过F1的直线垂直于x轴且与该双曲线相交于A，B两点，△ABF2 的内切圆经过点（0，a），则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
交通局对上班、下班高峰时的车速情况作抽样调查，行驶时速（单位：km/h）的统计数据用茎叶图表示如图：
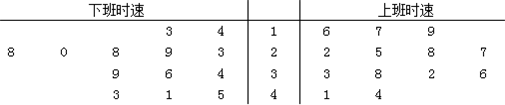
设上、下班时速的平均数分别为
上、
下，中位数分别为
上、
下，则（ ）
设上、下班时速的平均数分别为
. |
| x |
. |
| x |
. |
| m |
. |
| m |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
若θ为锐角且cosθ-cos-1θ=-2，则cosθ+cos-1θ的值为（ ）
A、2
| ||
B、
| ||
| C、6 | ||
| D、4 |
参数方程
（t为参数）表示什么曲线（ ）
|
| A、一条直线 | B、一个半圆 |
| C、一条射线 | D、一个圆 |
如图所示，四棱锥P-ABCD的底面ABCD是矩形，侧面PAD是等腰直角三角形，