题目内容
18．cos$\frac{17π}{6}$等于（ ）| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
分析 原式利用余弦函数为偶函数化简，将角度变形后利用诱导公式化简，计算即可得到结果．
解答 解：cos$\frac{17π}{6}$=cos（3π-$\frac{π}{6}$）=cos（π-$\frac{π}{6}$）=-cos$\frac{π}{6}$=-$\frac{\sqrt{3}}{2}$．
故选：C．
点评 此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键，属于基础题．
练习册系列答案
相关题目
9．已知函数f（x）=sin（ωx+φ）（0＜ω＜1，|φ|＜π）．若对任意x∈R，f（1）≤f（x）≤f（6），则（ ）
| A． | f（2014）-f（2017）＜0 | B． | f（2014）-f（2017）=0 | C． | f（2014）+f（2017）＜0 | D． | f（2014）+f（2017）=0 |
6．已知f（x）=|xex|，又g（x）=f2（x）-tf（x）（t∈R），若满足g（x）=-1的x有四个，则t的取值范围是（ ）
| A． | $（-∞，-\frac{{{e^2}+1}}{e}）$ | B． | $（\frac{{{e^2}+1}}{e}，+∞）$ | C． | $（-\frac{{{e^2}+1}}{e}，-2）$ | D． | $（2，\frac{{{e^2}+1}}{e}）$ |
13．已知全集U={-2，0，1，2}，集合A={x|x2-2x=0}，则∁UA=（ ）
| A． | {-2，1} | B． | {-2，0，2} | C． | {0，2} | D． | {0，1} |
3．双曲线的顶点到渐进线的距离等于虚轴长的$\frac{1}{4}$，则此双曲线的离心率是（ ）
| A． | 2 | B． | $\frac{3}{2}$ | C． | 3 | D． | 4 |
10．已知集合M={x|x＜2}，$N=\left\{{\left.x\right|{3^x}＞\frac{1}{3}}\right\}$，则M∩N=（ ）
| A． | ∅ | B． | {x|-1＜x＜2} | C． | {x|0＜x＜2} | D． | {x|1＜x＜2} |
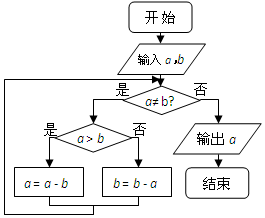如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为225，135，则输出的a=45．