题目内容
17.抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}+1}{2}$ | D. | $\sqrt{2}$+1 |
分析 确定抛物线y2=2px(p>0)的焦点与准线方程,利用点M为这两条曲线的一个交点,且|MF|=p,求出M的坐标,代入双曲线方程,即可求得结论.
解答 解:抛物线y2=2px(p>0)的焦点为F($\frac{p}{2}$,0),其准线方程为x=-$\frac{p}{2}$,
∵准线经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,
∴c=$\frac{p}{2}$;
∵点M为这两条曲线的一个交点,且|MF|=p,
∴M的横坐标为$\frac{p}{2}$,
代入抛物线方程,可得M的纵坐标为±p,
将M的坐标代入双曲线方程,可得$\frac{\frac{{p}^{2}}{4}}{{a}^{2}}-\frac{{p}^{2}}{{b}^{2}}$=1,
∴a=$\frac{\sqrt{2}-1}{2}$p,
∴e=1+$\sqrt{2}$.
故选:D.
点评 本题考查抛物线的几何性质,考查曲线的交点,考查双曲线的几何性质,确定M的坐标是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.命题“?x∈N,x2>x”的否定为( )
| A. | ?x∈N,x2≤x | B. | ?x0∈N,${x}_{0}^{2}$≤x0 | C. | ?x∉N,x2>x | D. | ?x0∉N,${x}_{0}^{2}$≤x0 |
5.某产品的广告费用x万元与销售额y万元的统计数据如表:
根据上表可得回归方程$\widehaty=9.4x+a$,据此模型预测,广告费用为6万元时的销售额为( )万元.
| 广告费用x | 2 | 3 | 4 | 5 |
| 销售额y | 26 | 39 | 49 | 54 |
| A. | 65.5 | B. | 66.6 | C. | 67.7 | D. | 72 |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点在直线x=6上,其中一条渐近线方程为y=$\sqrt{3}$x,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{108}$=1 | B. | $\frac{{x}^{2}}{108}$-$\frac{{y}^{2}}{36}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1 | D. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{9}$=1 |
2.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且当PA与抛物线相切时,点P恰好在以A、B为焦点的双曲线上,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{2}+1}}{2}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{5}-1$ |
9.函数f(x)=e2x+2cosx-4在[0,2π]上是( )
| A. | 在[0,π]上是减函数,[0,2π]上是增函数 | B. | [0,π]在上是增函数,[0,2π]上是减函数 | ||
| C. | 增函数 | D. | 减函数 |
14.已知图甲是函数f(x)的图象,图乙是由图甲变换所得,则图乙中的图象对应的函数可能是( )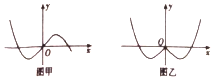
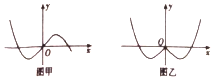
| A. | y=f(|x|) | B. | y=|f(x)| | C. | y=f(-|x|) | D. | y=-f(-|x|) |
15.若sinθ<cosθ,且sinθ•cosθ<0,则角θ的终边位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |