题目内容
设定义域为R的函数f(x)=
,若关于x的方程f(x)2+bf(x)+c=0有三个不同的实数根x1,x2,x3,则
+
+
等于( )
|
| x | 2 1 |
| x | 2 2 |
| x | 2 3 |
| A、5 | B、4 | C、1 | D、0 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:先画出f(x)的图象,观察图形可知若关于x的方程f2(x)+af(x)+b=3有三个不同实数解满足的条件,然后图象对称性求出三个根即可.
解答:
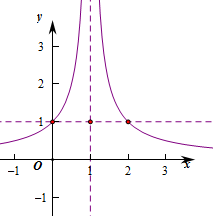 解:分段函数的图象如图所示:
解:分段函数的图象如图所示:
由图可知,只有当f(x)=1时,它有三个根.
由
=1,即|x-1|=1,
解得x=0,x=2或x=1.
∴关于x的方程f2(x)+af(x)+b=0有且只有3个不同实数解,
解分别是2,1,0,即x1=2,x2=1,x3=0,
∴x12+x22+x32=4+1+0=5,
故选:A.
 解:分段函数的图象如图所示:
解:分段函数的图象如图所示:由图可知,只有当f(x)=1时,它有三个根.
由
| 1 |
| |x-1| |
解得x=0,x=2或x=1.
∴关于x的方程f2(x)+af(x)+b=0有且只有3个不同实数解,
解分别是2,1,0,即x1=2,x2=1,x3=0,
∴x12+x22+x32=4+1+0=5,
故选:A.
点评:本题主要考查了函数与方程的综合运用,以及函数的图象与方程之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
若A={x|x2=x+2},则( )
| A、2∉A | B、-1∉A |
| C、2⊆A | D、-1∈A |
若集合M={0,1,2,3,4},N={x|x是偶数},则集合M∩N的子集个数为( )
| A、2 | B、4 | C、6 | D、8 |
方程x3-7x2+16x-12=0的实根的个数( )
| A、3 | B、2 | C、1 | D、0 |
若点(a,b)在y=lgx的图象上,a>0且a≠1,则下列点也在此图象上的是( )
A、(
| ||
| B、(10a,1-b) | ||
| C、(10+a,b+1) | ||
| D、(a2013,2013b) |
设函数y=f(x)是定义在R上以1为周期的函数,若g(x)=f(x)-2x在区间[2,3]上的值域为[-2,6],则函数g(x)在[-2012,2012]上的值域为( )
| A、[-2,6] |
| B、[-4030,4024] |
| C、[-4020,4034] |
| D、[-4028,4016] |
已知函数f(x)定义域为[-1,4],则f(3x-1)的定义域为( )
| A、[4,19] | ||
B、[
| ||
C、[0,
| ||
D、[
|
已知椭圆
+
=1(a>b>0),F1,F2为左、右焦点,A1、A2、B1、B2分别是其左、右、上、下顶点,直线B1F2交直线B2A2于P点,若∠B1PA2为直角,则此椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合p={x|(x-1)(x-3)≤0},Q={x||x|<2},则p∪Q等于( )
| A、[1,2) |
| B、[1,3] |
| C、(-2,3] |
| D、(-2,2) |