题目内容

圆x2+y2+2y=1的圆心为（　　）
A、（0，1）
B、（0，-1）
C、（0，2）
D、（0，-2）
考点：圆的一般方程
专题：计算题,直线与圆
分析：首先根据圆的一般式方程改写成圆的标准方程，进而由圆的标准方程得到圆的圆心坐标．
解答： 解：由题意可得：圆的方程为：x2+y2+2y=1，
所以圆的标准方程为：x2+（y+1）2=2，
所以圆的圆心为（0，-1）．
故选：B．
点评：解决此类问题的关键是熟练掌握圆的一般方程与标准方程之间的相互转化，并且结合正确的运算．
练习册系列答案
相关题目
设函数f（x）=lnx-
1
2
ax2-bx（a≤0）．
（Ⅰ）若x=1是f（x）的极大值点，求a的取值范围；
（Ⅱ）当a=0，b=-1时，函数g（x）=mx2-f（x）有唯一零点，求实数m的取值范围．
已知抛物线C：y=
1
4
x2，则其焦点坐标为
 
；准线方程为
 
．
已知tanα=
2
，sin（α+β）=
5
13
，α，β∈（0，π），求cosβ．
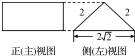如图是一个几何体的正（主）视图和侧（左）视图，其俯视图是面积为8
2
的矩形，则该几何体的表面积是（　　）
A、20+8
2
B、24+8
2
C、8
D、16
已知等比数列{an}满足：a2+a3+a4=28，且a3+2是a2，a4的等差中项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{an}是单调递增的，令bn=anlog 
1
2
an，Sn=b1+b2+…+bn，求使Sn+n2n+1＞50成立的正整数n的最小值．
定义 A+B={x+y|x∈A，y∈B}，设集合 M={0，1+i}，N={0，
-1-3i
2+i
}，则集合 M+N中元素的个数为（　　）
A、4B、3C、2D、1
命题“?a，b∈R，如果a=b，则a2=ab”的否命题为（　　）
A、?a，b∈R，如果a2=ab，则a=b
B、?a，b∈R，如果a2=ab，则a≠b
C、?a，b∈R，如果a2≠ab，则a≠b
D、?a，b∈R，如果a≠b，则a2≠ab
在等比数列{an}中，a4=4，则a2•a6=（　　）
A、32B、16C、8D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网