题目内容
先将下列代数式化简,再求值:(a+b)(a-b)+b(b-2),其中a=
,b=1.
| 2 |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:利用多项式的乘法运算即可得出.
解答:
解:(a+b)(a-b)+b(b-2)=a2-b2+b2-2b=a2-2b.
把a=
,b=1代入可得:原式=(
)2-2×1=0
把a=
| 2 |
| 2 |
点评:本题考查了多项式的乘法运算,属于基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
已知数列{an}满足:a1=1,
=
,n∈N*,{an}的前项和为Sn,则( )
| 1 |
| an+1 |
| 1 |
| 2an |
A、Sn=2-(
| ||
B、Sn=2-(
| ||
| C、Sn=2n-1 | ||
| D、Sn=2n-1-1 |
下列集合中表示同一集合的是( )
| A、M={(3,2)},N={(2,3)} |
| B、M={(x,y)|x+y=1},N={y|x+y=1} |
| C、M={4,5},N={5,4} |
| D、M={1,2},N={(1,2)} |
已知函数f(x)=ax3+bx2+cx+d(a≠0)的对称中心为M(x0,y0),记函数f(x)的导函数为f′(x),f′(x)的导函数为f″(x),则有f″(x0)=0.若函数f(x)=x3-3x2,则可求出f(
)+f(
)+f(
)+…+f(
)+f(
)的值为( )
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4028 |
| 2015 |
| 4029 |
| 2015 |
| A、4029 | B、-4029 |
| C、8058 | D、-8058 |
二进制数1111111111转化为十进制数应该是( )
| A、1023 | B、1024 |
| C、2047 | D、2048 |
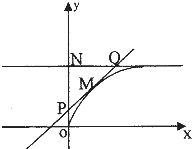 如图为函数f(x)=
如图为函数f(x)=