题目内容
求函数y=(x+1)(x+2)(x+3)(x+4)+5在区间[-2,1]上的最大值和最小值.
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:原函数可化为y=(x2+5x+5)2+4,即可得出结论.
解答:
解:y=(x+1)(x+2)(x+3)(x+4)+5
=(x+1)(x+2)(x+3)(x+4)+5
=(x+1)(x+4)(x+2)(x+3)+5
=[(x+1)(x+4)][(x+2)(x+3)]+5
=(x2+5x+4)(x2+5x+6)+5
=(x2+5x+4)(x2+5x+4+2)+1+4
=(x2+5x+4)2+2(x2+5x+4)+1+4
=(x2+5x+4+1)2+4
=(x2+5x+5)2+4
∴当x2+5x+5=0即
时,ymin=4,
当x=1时,ymax=11.
=(x+1)(x+2)(x+3)(x+4)+5
=(x+1)(x+4)(x+2)(x+3)+5
=[(x+1)(x+4)][(x+2)(x+3)]+5
=(x2+5x+4)(x2+5x+6)+5
=(x2+5x+4)(x2+5x+4+2)+1+4
=(x2+5x+4)2+2(x2+5x+4)+1+4
=(x2+5x+4+1)2+4
=(x2+5x+5)2+4
∴当x2+5x+5=0即
| ||
| 2 |
当x=1时,ymax=11.
点评:本题考查函数的最值问题,注意式子的合理变形,是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知函数f(x)=x2+(m-2)x+m2+12为偶函数,则m的值是( )
| A、1 | B、2 | C、3 | D、4 |
一个圆锥体按如图所示摆放,它的主视图是( )


A、 |
B、 |
C、 |
D、 |
如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
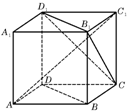

| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AC1与CB所成的角为60° |
已知命题p:x≥1,命题q:x2≥x,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |



