已知等比数列{an}中.a2a4=a5.a4=8.则公比q=2.其前4项和S4=15．题目和参考答案——青夏教育精英家教网——

题目内容

1．已知等比数列{a_n}中，a₂a₄=a₅，a₄=8，则公比q=2，其前4项和S₄=15．

分析设等比数列{a_n}的公比为q，由a₂a₄=a₅，a₄=8，可得${a}_{2}^{2}$q²=a₂q³，${a}_{2}{q}^{2}$=8，解得a₂，q，利用求和公式即可得出．

解答解：设等比数列{a_n}的公比为q，∵a₂a₄=a₅，a₄=8，
∴${a}_{2}^{2}$q²=a₂q³，${a}_{2}{q}^{2}$=8，解得a₂=q=2．
∴a₁=1．
其前4项和S₄=$\frac{1×（{2}^{4}-1）}{2-1}$=15．
故答案为：2，15．

点评本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

金博优题典单元练测活页卷系列答案

DIY英语系列答案

晨光全优口算应用题天天练系列答案

提优检测卷初中强化拓展系列答案

百渡中考必备中考试题精选系列答案

魅力语文系列答案

状元龙初中语文现代文阅读系列答案

初中现代文文言文拓展阅读系列答案

启光中考全程复习方案系列答案

授之以渔中考试题汇编系列答案

相关题目

11．（3a+2b）⁶的展开式中的第3项的二项式系数为15．（用数字作答）

12．已知在平面直角坐标系中，曲线C₁的参数方程是$\left\{\begin{array}{l}x=-1+cosθ\\ y=sinθ\end{array}\right.$（θ为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线C₂的极坐标方程是ρ=2sinθ．
（Ⅰ）求曲线C₁与C₂交点的平面直角坐标；
（Ⅱ）点A，B分别在曲线C₁，C₂上，当|AB|最大时，求△OAB的面积（O为坐标原点）．

9．等比数列{a_n}中各项均为正数，S_n是其前n项和，且满足2S₃=8a₁+3a₂，a₄=16，则S₄=（　　）

16．圆心为（0，1）且与直线y=2相切的圆的方程为（　　）

（x-1）²+y²=1

（x+1）²+y²=1

x²+（y-1）²=1

x²+（y+1）²=1

6．某地区以“绿色出行”为宗旨开展“共享单车”业务．该地有a，b两种“共享单车”（以下简称a型车，b型车）．某学习小组7名同学调查了该地区共享单车的使用情况．
（Ⅰ）某日该学习小组进行一次市场体验，其中4人租到a型车，3人租到b型车．如果从组内随机抽取2人，求抽取的2人中至少有一人在市场体验过程中租到a型车的概率；
（Ⅱ）根据已公布的2016年该地区全年市场调查报告，小组同学发现3月，4月的用户租车情况城现如表使用规律．例如，第3个月租a型车的用户中，在第4个月有60%的用户仍租a型车．

第3个月第4个月	租用a型车	租用b型车
租用a型车	60%	50%
租用b型车	40%	50%

若认为2017年该地区租用单车情况与2016年大致相同．已知2017年3月该地区租用a，b两种车型的用户比例为1：1，根据表格提供的信息，估计2017年4月该地区租用两种车型的用户比例．

13．数列{a_n}中，已知a₁=1，a₂=a，a_n+1=k（a_n+a_n+2）对任意n∈N^*都成立，数列{a_n}的前n项和为S_n．（这里a，k均为实数）
（1）若{a_n}是等差数列，求S_n；
（2）若a=1，k=-$\frac{1}{2}$，求S_n；
（3）是否存在实数k，使数列{a_n}是公比不为1的等比数列，且任意相邻三项a_m，a_m+1，a_m+2按某顺序排列后成等差数列？若存在，求出所有k的值；若不存在，请说明理由．

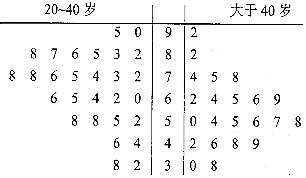某公司即将推车一款新型智能手机，为了更好地对产品进行宣传，需预估市民购买该款手机是否与年龄有关，现随机抽取了50名市民进行购买意愿的问卷调查，若得分低于60分，说明购买意愿弱；若得分不低于60分，说明购买意愿强，调查结果用茎叶图表示如图所示．
（1）根据茎叶图中的数据完成2×2列联表，并判断是否有95%的把握认为市民是否购买该款手机与年龄有关？

	购买意愿强	购买意愿弱	合计
20-40岁
大于40岁
合计

（2）从购买意愿弱的市民中按年龄进行分层抽样，共抽取5人，从这5人中随机抽取2人进行采访，记抽到的2人中年龄大于40岁的市民人数为X，求X的分布列和数学期望．
附：${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

P（K²≥k₀）	0.100	0.050	0.010	0.001
k₀	2.706	3.841	6.635	10.828

18．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，点P（x₀，$\frac{5}{2}$）为双曲线上一点，若△PF₁F₂的内切圆半径为1，且圆心G到原点O的距离为$\sqrt{5}$，则双曲线的方程为（　　）

$\frac{{x}^{2}}{3}$-$\frac{8{y}^{2}}{25}$=1

$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1

$\frac{{x}^{2}}{6}$-$\frac{2{y}^{2}}{25}$=1

$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{50}$=1