题目内容
6.设公差不为零的等差数列{an}的前n项和为Sn,若a4=2(a2+a3),则$\frac{S_7}{S_4}$=( )| A. | $\frac{7}{4}$ | B. | $\frac{14}{5}$ | C. | 7 | D. | 14 |
分析 利用等差数列的通项公式及其前n项和公式即可得出.
解答 解:∵a4=2(a2+a3),∴a4=2(a1+a4),
则$\frac{S_7}{S_4}$=$\frac{\frac{7({a}_{1}+{a}_{7})}{2}}{\frac{4({a}_{1}+{a}_{4})}{2}}$=$\frac{7×2{a}_{4}}{4({a}_{1}+{a}_{4})}$=7.
故选:C.
点评 本题考查了等差数列的通项公式性质及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
16.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )
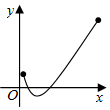

| A. | f(x)=2x+lgx+2 | B. | f(x)=2x+lgx-2 | C. | f(x)=2x-lgx+2 | D. | f(x)=2x-lgx-2 |
17.在正项等比数列{an}中,若3a1,$\frac{1}{2}$a3,2a2成等差数列,则$\frac{{a}_{2016}-{a}_{2017}}{{a}_{2014}-{a}_{2015}}$=( )
| A. | 3或-1 | B. | 9或1 | C. | 3 | D. | 9 |
1.已知i为虚数单位,a∈R,若(a2+2a-3)+(a+3)i为纯虚数,则a的值为( )
| A. | 1 | B. | -3 | C. | -3或1 | D. | 3或1 |
15.复数$\frac{2}{(1-i)i}$(i为复数单位)的共轭复数为( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |