题目内容
一物体在力F(x)=
(单位:N)的作用下沿与力F相同的方向,从x=0处运动到x=4(单位:m)处,则力F(x)做的功为( )焦.
|
| A、16 | B、20 | C、36 | D、40 |
考点:定积分
专题:导数的概念及应用
分析:本题是一个求变力做功的问题,可以利用积分求解,由题意,其积分区间是[0,1],被积函数是力的函数表达式,由积分公式进行计算即可得到答案
解答:
解:W=
F(x)dx=
5dx+
(3x+4)dx=5x
+(
x2+4x)
=36.
故选:C.
| ∫ | 4 0 |
| ∫ | 2 0 |
| ∫ | 4 2 |
| | | 2 0 |
| 3 |
| 2 |
| | | 4 2 |
故选:C.
点评:本题考查定积分的应用,物理中的变力所做的功用定积分求解是定积分在物理中的重要应用,正确解答本题的关键是理解功与定积分的对应.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
函数y=ln(2x2+1)的导数是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(n)=
,且an=f(n)+f(n+1),则a1+a2+…+a2014的值为( )
|
| A、0 | B、2014 |
| C、-2014 | D、2014×2015 |
已知空间三点A(1,1,1),B(-1,0,4),C(2,-2,3),则向量
与
的夹角为( )
| AB |
| CA |
| A、60° | B、30° |
| C、120° | D、300° |
已知函数f(x)=
的定义域为R,则实数a的取值范围是( )
| x+1 |
| a2x-2x+a |
| A、a<-1或a>1 |
| B、a>1 |
| C、a<-1 |
| D、a>1或a=0或a<-1 |
已知x与y之间的一组数据:
则y与x的线性回归方程为
=bx+a必过点( )
| x | 1 | 2 | 3 | 4 |
| y | 2 | 3 | 5 | 8 |
 |
| y |
| A、(4.5,2.5) |
| B、(1.5,4.5) |
| C、(2.5,4.5) |
| D、(1.5,4) |
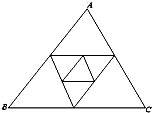 如图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,设第n个三角形周长为l(n),则归纳l(n)关于n的表达式为l(n)=
如图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,设第n个三角形周长为l(n),则归纳l(n)关于n的表达式为l(n)=