题目内容
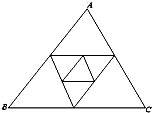 如图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,设第n个三角形周长为l(n),则归纳l(n)关于n的表达式为l(n)=
如图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,设第n个三角形周长为l(n),则归纳l(n)关于n的表达式为l(n)=考点:归纳推理
专题:推理和证明
分析:根据三角形的中位线定理,找规律求解,每一条中位线均为其对应的边的长度的
,所以新三角形周长是前一个三角形的
.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:△ABC周长为1,因为每条中位线均为其对应边的长度的
,
所以:第2个三角形对应周长为
第3个三角形对应的周长为
×
=(
)2
第4个三角形对应的周长为
×
×
=(
)3
…
以此类推,第n个三角形对应的周长为(
)n-1
故答案为:.(
)n-1(n∈N*)
| 1 |
| 2 |
所以:第2个三角形对应周长为
| 1 |
| 2 |
第3个三角形对应的周长为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
第4个三角形对应的周长为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
…
以此类推,第n个三角形对应的周长为(
| 1 |
| 2 |
故答案为:.(
| 1 |
| 2 |
点评:本题考查了三角形中位线定理,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足(2a-c)cosB=bcosC.则角B为( )
| A、30° | B、60° |
| C、120° | D、150° |
点P(x,y)是椭圆6x2+3y2=12上的一个动点,则x+2y的最大值为( )
A、2
| ||
B、3
| ||
C、2
| ||
D、3
|