题目内容
12．在（1+x3）（1-x）8的展开式中，x5的系数是（ ）| A． | -28 | B． | -84 | C． | 28 | D． | 84 |
分析 利用二项式定理的通项公式求解即可．
解答 解：由（1+x3）展开可知含有x3与（1-x）8展开的x2可得x5的系数；
由（1+x3）展开可知常数项与（1-x）8展开的x5，同样可得x5的系数；
∴含x5的项：${C}_{3}^{3}{x}^{3}{•C}_{8}^{2}{x}^{2}$+${C}_{3}^{0}{{x}^{0}C}_{8}^{5}{x}^{5}（-1）^{3}$=28x5-56x5=-28x5；
∴x5的系数为-28，
故选A
点评 本题主要考查二项式定理的应用，求展开式的系数把含有x5的项找到．从而可以利用通项求解．属于中档题
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
3．某校对学生的思想品德、学业成绩、社会实践能力进行综合评价，思想品德、学业成绩、社会实践能力评价指数分别记为x，y，z，每项评价指数都为1分、2分、3分、4分、5分五等，综合评价指标S=x+y+z，若S≥13，则该学生为优秀学生．现从该校学生中，随机抽取10名学生作为样本，分为A，B两组，其评价指数列表如下：
A组
B组
（1）从A，B两组中各选一名学生，依次记为甲、乙，求乙的综合评价指标大于甲的综合评价指标的概率；
（2）若该校共有1500名学生，估计该校有多少名优秀学生．
A组
| 学生编号 | A1 | A2 | A3 | A4 | A5 |
| 评价指数（x，y，z） | （3，4，3） | （4，3，4） | （4，4，2） | （4，3，5） | （4，5，4） |
| 学生编号 | B1 | B2 | B3 | B4 | B5 |
| 评价指数（x，y，z） | （3，5，3） | （4，3，2） | （5，4，4） | （5，4，5） | （4，5，3） |
（2）若该校共有1500名学生，估计该校有多少名优秀学生．
20．在△ABC中，∠BAC的平分线交BC边于D，若AB=2，AC=1，则△ABD面积的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | 1 |
7．已知A，B是半径为$2\sqrt{3}$的球面上的两点，过AB作互相垂直的两个平面α、β，若α，β截该球所得的两个截面的面积之和为16π，则线段AB的长度是（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $2\sqrt{2}$ | D． | 4 |
17．设i是虚数单位，若复数$z=\frac{3+i}{1+i}$，则复数z的实部为（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -3 |
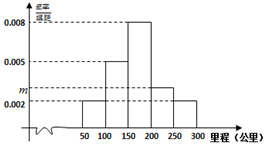绿色出行越来越受到社会的关注，越来越多的消费者对新能源汽车感兴趣．但是消费者比较关心的问题是汽车的续驶里程．某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：[50，100），[100，150），[150，200），[200，250），[250，300]，绘制成如图所示的频率分布直方图．