题目内容
(本小题满分12分)
如图,三棱锥 中,
中, 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若 ,
, 为
为 中点,求三棱锥
中点,求三棱锥 的体积.
的体积.
(1)见解析.(2)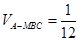 .
.
解析试题分析:
(1)由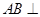 平面BCD,
平面BCD, 平面BCD,
平面BCD,
得到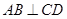 .
.
进一步即得 平面
平面 .
.
(2)思路一:由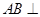 平面BCD,得
平面BCD,得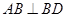 .
.
确定 .
.
根据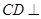 平面ABD,
平面ABD,
知三棱锥C-ABM的高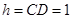 ,
,
得到三棱锥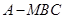 的体积
的体积 .
.
思路二:由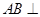 平面BCD知,平面ABD
平面BCD知,平面ABD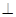 平面BCD,
平面BCD,
根据平面ABD 平面BCD=BD,
平面BCD=BD,
通过过点M作 交BD于点N.
交BD于点N.
得到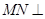 平面BCD,且
平面BCD,且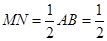 ,
,
利用 计算三棱锥
计算三棱锥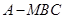 的体积.
的体积.
试题解析:解法一:
(1)∵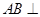 平面BCD,
平面BCD, 平面BCD,
平面BCD,
∴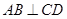 .
.
又∵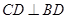 ,
,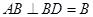 ,
,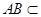 平面ABD,
平面ABD, 平面ABD,
平面ABD,
∴ 平面
平面 .
.
(2)由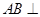 平面BCD,得
平面BCD,得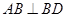 .
.
∵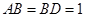 ,∴
,∴ .
.
∵M是AD的中点,
∴ .
.
由(1)知,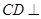 平面ABD,
平面ABD,
∴三棱锥C-ABM的高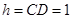 ,
,
因此三棱锥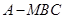 的体积
的体积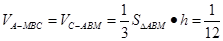 .
.
解法二:
(1)同解法一.
(2)由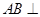 平面BCD知,平面ABD
平面BCD知,平面ABD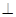 平面BCD,
平面BCD,
又平面ABD 平面BCD=BD,
平面BCD=BD,
如图,过点M作 交BD于点N.
交BD于点N.
则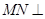 平面BCD,且
平面BCD,且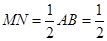 ,
,
又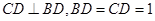 ,
,
∴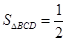 .
.
∴三棱锥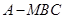 的体积
的体积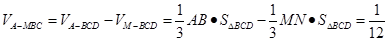 .
.
考点:垂直关系,几何体的体积,“间接法”、“等积法”.

练习册系列答案
相关题目
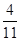
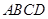 是菱形,
是菱形,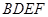 是矩形,
是矩形,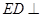 面
面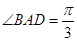 .
.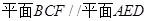 .
.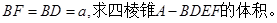

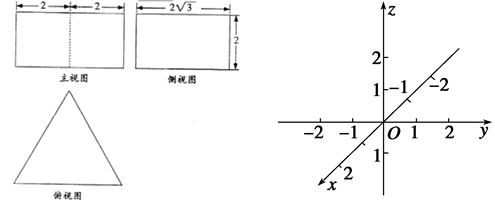
 的棱长为
的棱长为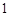 .
.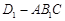 的左视图的面积;
的左视图的面积;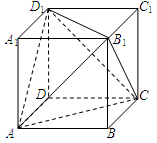
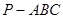 中,平面
中,平面 平面
平面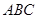 ,
,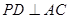 于点
于点 ,且
,且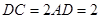 ,
,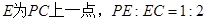 ,
, 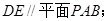
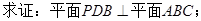
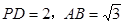 ,
,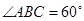 ,求三棱锥
,求三棱锥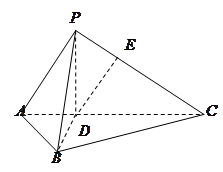
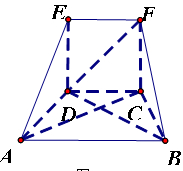
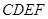 为正方形,四边形
为正方形,四边形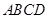 为等腰梯形,
为等腰梯形,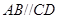 ,
,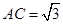 ,
,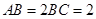 ,
,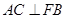 .
.
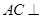 平面
平面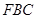 ;
;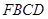 的体积;
的体积; 上是否存在点
上是否存在点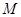 ,使
,使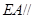 平面
平面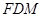 ?请证明你的结论.
?请证明你的结论. 为圆心,以
为圆心,以 为半径的圆的方程为
为半径的圆的方程为 ,类似的在空间以点
,类似的在空间以点 为球心,以
为球心,以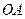 为球
为球 的半径,过
的半径,过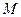 且垂直于
且垂直于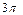 ,则球
,则球