题目内容
17.给出下列函数①$f(x)=(\frac{1}{2})^{x}$; ②f(x)=x2; ③f(x)=x3; ④$f(x)={x}^{\frac{1}{2}}$;⑤f(x)=log2x.其中满足条件f $(\frac{{x}_{1}+{x}_{2}}{2})$>$\frac{f({x}_{1})+f({x}_{2})}{2}$ (0<x1<x2)的函数的序号是④⑤.分析 分别作出函数①$f(x)=(\frac{1}{2})^{x}$; ②f(x)=x2; ③f(x)=x3; ④$f(x)={x}^{\frac{1}{2}}$;⑤f(x)=log2x的图象,数形结合可得答案.
解答 解:若满足条件f $(\frac{{x}_{1}+{x}_{2}}{2})$>$\frac{f({x}_{1})+f({x}_{2})}{2}$ (0<x1<x2),则函数f(x)的图象为上凸形,
分别作出函数①$f(x)=(\frac{1}{2})^{x}$; ②f(x)=x2; ③f(x)=x3; ④$f(x)={x}^{\frac{1}{2}}$;⑤f(x)=log2x的图象,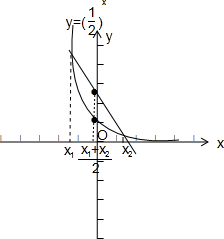
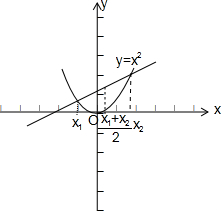

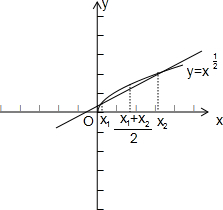
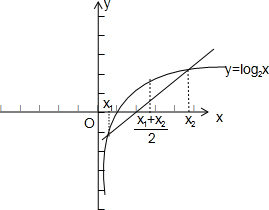 ,
,
数形结合可得,只有④、⑤满足条件,
故答案为:④⑤.
点评 本题考查命题的真假判断与应用,着重考查幂函数、指数函数、对数函数、三角函数的图象与性质,作图分析是关键,属于基础题.

练习册系列答案
相关题目
8.在△ABC中,若c=2acosB,则△ABC的形状一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 等腰或直角三角形 | D. | 等腰三角形 |
12.已知函数f(x)=lnx+$\frac{1}{2}$ax2-2x有两个极值点,则a的取值范围是( )
| A. | (-∞,1) | B. | (0,2) | C. | (0,1) | D. | (0,3) |
2.设函数f(x)=$\left\{{\begin{array}{l}{{2^x},x≤0}\\{{{log}_2}x,x>0}\end{array}}$,则函数y=f[f(x)]的零点个数为( )
| A. | 1个 | B. | 2个 | C. | 3 个 | D. | 4个 |
6.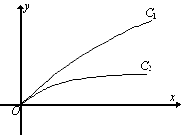 如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )
如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )
 如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )
如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )| A. | 0<λ2<λ1 | B. | λ2<λ1<0 | C. | λ1<λ2<0 | D. | 0<λ1<λ2 |
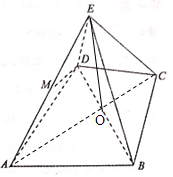 如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD,
如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD,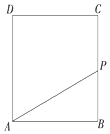 如图所示,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过顶点B,C,D再回到A.设x表示P点的路程,y表示PA的长度,求y关于x的函数关系式.
如图所示,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过顶点B,C,D再回到A.设x表示P点的路程,y表示PA的长度,求y关于x的函数关系式.