题目内容
13.已知正方体ABCD-A1B1C1D1,设棱长为a,过BD且与直线AC1平行的截面面积是( )| A. | $\frac{a^2}{2}$ | B. | $\frac{{\sqrt{6}}}{4}{a^2}$ | C. | $\frac{{\sqrt{3}}}{4}{a^2}$ | D. | $\frac{{\sqrt{3}}}{2}{a^2}$ |
分析 如图连结AC交BD与O,连结OE,由OE∥AC1,得AC1∥平面BDE,求出△BDE的面积即可.
解答 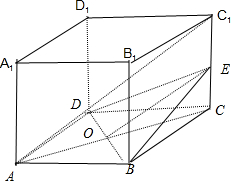 解:如图连结AC交BD与O,连结OE,
解:如图连结AC交BD与O,连结OE,
因为O、E分别是AC、CC1的中点,
∴OE∥AC1,
又因为OE?平面BDE,AC1?平面BDE.
∴AC1∥平面BDE,∴△DBE就是过BD且与直线AC1平行的截面.
易得△DBE是等腰△,且DB⊥OE
在△DBE中,BD=$\sqrt{2}a$,OE=$\sqrt{O{C}^{2}+C{E}^{2}}=\frac{\sqrt{3}}{2}a$
∴${S}_{△DBE}=\frac{1}{2}×DB×OE=\frac{1}{2}×\sqrt{2}a×$$\frac{\sqrt{3}}{2}a$=$\frac{\sqrt{6}}{4}{a}^{2}$.
故选:B.
点评 本题考查了线线垂直、线面平行的判定,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
4.已知复数z的共轭复数记为$\overline z,i$为虚数单位,若(1+2i)$\overline z$=4-3i,复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.若log9(3a+4b)=log3$\sqrt{ab}$,则a+b的最小值是( )
| A. | $6+2\sqrt{3}$ | B. | $7+2\sqrt{3}$ | C. | $6+4\sqrt{3}$ | D. | $7+4\sqrt{3}$ |
18. 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )| A. | $\frac{5}{4}$ | B. | $\frac{24}{7}$ | C. | $-\frac{21}{24}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
2.已知函数$f(x)=lnx-x+\frac{1}{x}$,若a=f(3),b=f(π),c=f(5),则( )
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | a<c<b |
3.a,b为正实数,若函数f(x)=ax3+bx+ab-1是奇函数,则f(2)的最小值是( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
