题目内容
17.已知A1,A2分别为双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的左、右顶点,P为双曲线上第一限内的点,直线l:x=1与x轴交于点C,若直线PA1,PA2分别交直线l于B1,B2两点,且△A1B1C与A2B2C的面积相等,则直线PA1的斜率为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{3}$ |
分析 设P(m,n),(m,n>0),代入双曲线的方程,求得左右顶点和两直线的方程,可令x=1,求得交点B1,B2两点的坐标,运用直角三角形的面积公式解方程可得m,进而得到n的值,可得直线PA1的斜率.
解答 解:设P(m,n),(m,n>0),即有$\frac{{m}^{2}}{4}$-$\frac{{n}^{2}}{9}$=1,①
由题意可得A1(-2,0),A2(2,0),
直线PA1的方程为y=$\frac{n}{m+2}$(x+2),
令x=1可得y=$\frac{3n}{m+2}$;
直线PA2的方程为y=$\frac{n}{m-2}$(x-2),
令x=1可得y=-$\frac{n}{m-2}$.
由直角三角形的面积公式可得
$\frac{1}{2}$•3•$\frac{3n}{m+2}$=$\frac{1}{2}$•1•$\frac{n}{m-2}$,
解得m=$\frac{5}{2}$,
代入①可得n=$\frac{9}{4}$,
则直线PA1的斜率为$\frac{n}{m+2}$=$\frac{\frac{9}{4}}{\frac{5}{2}+2}$=$\frac{1}{2}$.
故选:B.
点评 本题考查直线的斜率的求法,注意运用点满足双曲线的方程,联立直线方程求交点,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
2.将一颗质地均匀的骰子(一种各面上分别标有1、2、3、4、5、6的正方体玩具),先后抛掷3次,至少出现一次4点向上的概率是( )
| A. | $\frac{5}{216}$ | B. | $\frac{31}{216}$ | C. | $\frac{91}{216}$ | D. | $\frac{25}{216}$ |
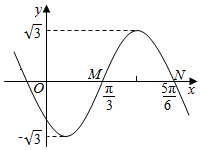 如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.
如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.