题目内容
已知A(2,0),B,C为圆x2+y2=4上两点,∠BAC=60°.
(1)求B,C中点轨迹方程.
(2)求△ABC重心轨迹方程.
(1)求B,C中点轨迹方程.
(2)求△ABC重心轨迹方程.
考点:轨迹方程,圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)将圆周角为定值转化为圆心角为定值,结合圆心距构成的直角三角形得OD=1,从而得BC中点的轨迹方程.
解答:
解:(1)设BC中点是D,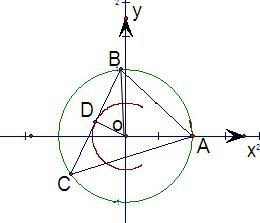
∵圆心角等于圆周角的一半,
∴∠BOD=60°,
∵BO=CO,
∴OD⊥BC,
在直角三角形BOD中,有OD=
OB=1,
故中点D的轨迹方程是:x2+y2=1,
如图,由角BAC的极限位置可得,x<
,
(2)设B点坐标为(2cost,2sint),C点坐标为(2cos(t+120°,2sin(t+120°)),三角形ABC重心坐标设为
(x,y),
则x=
(2+2cost+2cos(t+120°)),y=
(0+2sint+2sin(t+120°)),
3x-2=2cos(t-60°),3y=2cos(t-30°),
因此(3x-2)2+9y2=4,
这就是重心轨迹方程.

∵圆心角等于圆周角的一半,
∴∠BOD=60°,
∵BO=CO,
∴OD⊥BC,
在直角三角形BOD中,有OD=
| 1 |
| 2 |
故中点D的轨迹方程是:x2+y2=1,
如图,由角BAC的极限位置可得,x<
| 1 |
| 2 |
(2)设B点坐标为(2cost,2sint),C点坐标为(2cos(t+120°,2sin(t+120°)),三角形ABC重心坐标设为
(x,y),
则x=
| 1 |
| 3 |
| 1 |
| 3 |
3x-2=2cos(t-60°),3y=2cos(t-30°),
因此(3x-2)2+9y2=4,
这就是重心轨迹方程.
点评:本题主要考查求轨迹方程,解决与平面几何有关的轨迹问题时,要充分考虑到图形的几何性质,这样会使问题的解决简便些.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
下列三个数a=ln
-
,b=lnπ-π,c=ln3-3,大小顺序正确的是( )
| 3 |
| 2 |
| 3 |
| 2 |
| A、b>c>a |
| B、a>b>c |
| C、a>c>b |
| D、b>a>c |
等比数列{an}中,a1=
,公比q=2,设pn=a1•a2•a3…an,则当pn取最小值时,n的值为( )
| 1 |
| 1002 |
| A、8 | B、9 | C、10 | D、11 |
已知集合M={x|-3<x<1},N={x|x≤-3},则M∪N( )
| A、∅ |
| B、{x|x≥-3} |
| C、{x|x≥1} |
| D、{x|x<1} |