题目内容
(2012•九江一模)已知f(x)是定义在(0,+∞)上的单调函数,且对任意的x∈(0,+∞),都有f[f(x)﹣x3]=2,则方程f(x)﹣f′(x)=2的解所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
D
【解析】
试题分析:由题意,可知f(x)﹣x3是定值令t=f(x)﹣x3,得出f(x)=x3+t,再由f(t)=t3+t=2求出t的值即可得出f(x)的表达式,求出函数的导数,即可求出f(x)﹣f′(x)=2的解所在的区间选出正确选项
【解析】
由题意,可知f(x)﹣x3是定值,不妨令t=f(x)﹣x3,则f(x)=x3+t
又f(t)=t3+t=2,整理得(t﹣1)(t2+t+2)=0,解得t=1
所以有f(x)=x3+1
所以f(x)﹣f′(x)=x3+1﹣3x2=2,令F(x)=x3﹣3x2﹣1
可得F(3)=﹣1<0,F(4)=8>0,即F(x)=x3﹣3x2﹣1零点在区间(3,4)内
所以f(x)﹣f′(x)=2的解所在的区间是(3,4)
故选D

练习册系列答案
相关题目
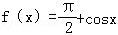 ,则f′(
,则f′(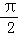 )=( )
)=( ) ex(sinx+cosx)在区间[0,
ex(sinx+cosx)在区间[0, ]上的值域为( )
]上的值域为( ) e
e ] B.(
] B.(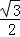 B.
B.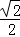 C.
C.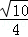 D.
D.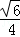
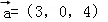 同向共线的单位向量
同向共线的单位向量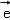 为( )
为( )
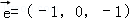
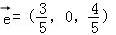
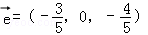
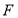 是椭圆
是椭圆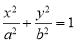 (
(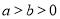 )的左焦点,
)的左焦点,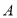 为右顶点,
为右顶点,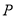 是椭圆上一点,
是椭圆上一点,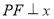 轴.若
轴.若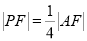 ,则该椭圆的离心率是( )
,则该椭圆的离心率是( ) (B)
(B) (C)
(C) (D)
(D)