题目内容
在三棱锥P﹣ABC中,PA=PB=PC=5,AB=3,AC=4,BC=5,则PA与平面ABC所成的角为( )
A.30° B.45° C.60° D.90°
C
【解析】
试题分析:过P作PD⊥平面ABC,垂足为D,先证明D是BC的中点,∠PBC为PA与平面ABC所成的角,从而可得结论.
【解析】
过P作PD⊥平面ABC,垂足为D,

∵AB=3,AC=4,BC=5,∴AB⊥AC
∵PA=PB=PC=,∴D是BC的中点
∴∠PBC为PA与平面ABC所成的角
∴PB=PC=BC,∴∠PBC=60°
故选C.

练习册系列答案
相关题目
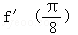 =( )
=( ) C.﹣1 D.﹣2
C.﹣1 D.﹣2
 B.
B. C.
C. D.
D.
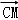 ,
, >的值为( )
>的值为( )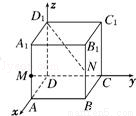
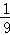 B.
B.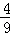
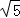 C.
C.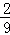
 D.
D.