题目内容
16.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右顶点分别是A1、A2,线段A1A2被抛物线y2=bx的焦点分为3:1两段,则此双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{5}-1$ |
分析 由题意可知$a+\frac{b}{4}$=$3(a-\frac{b}{4})$,化简得b=2a,由此导出c2=5a2,从而得到此双曲线的离心率.
解答 解:抛物线y2=bx的焦点坐标为$(\frac{b}{4},0)$,由题意知$a+\frac{b}{4}$=$3(a-\frac{b}{4})$,化简得b=2a,
即b2=4a2,又c2=a2+b2,
那么c2=5a2,于是$e=\frac{c}{a}=\sqrt{5}$.
故选:B.
点评 本题综合考查抛物线的焦点坐标和双曲线的离心率,解题的关键是恰当选用公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.当n=4时,执行如图所示的程序框图,输出S的值是( )


| A. | 7 | B. | 9 | C. | 11 | D. | 16 |
5.已知抛物线y2=2px(p>0)上一点M (x0,4)到焦点F 的距离|MF|=$\frac{5}{4}$x0,则直线 MF 的斜率kMF=( )
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
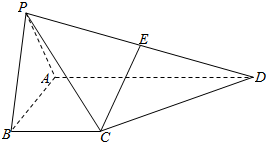 如图,在四棱锥P-ABCD 中,侧面PAB 为正三角形,侧面PAB⊥底面ABCD,E 为PD 的中点,AB⊥AD,BC∥AD,且AB=BC=$\frac{1}{2}$AD=2.
如图,在四棱锥P-ABCD 中,侧面PAB 为正三角形,侧面PAB⊥底面ABCD,E 为PD 的中点,AB⊥AD,BC∥AD,且AB=BC=$\frac{1}{2}$AD=2.