题目内容
10．若x+2y+4z=1，则x2+y2+z2的最小值是（ ）| A． | 21 | B． | $\frac{1}{21}$ | C． | 16 | D． | $\frac{1}{16}$ |
分析 由条件利用柯西不等式可得（x2+y2+z2）（1+4+16）≥（x+2y+4z）2=1，由此求得x2+y2+z2的最小值．
解答 解：∵x+2y+4z=1，利用柯西不等式可得（x2+y2+z2）（1+4+16）≥（x+2y+4z）2=1，
故x2+y2+z2≥$\frac{1}{21}$，当且仅当$\frac{x}{1}$=$\frac{y}{2}$=$\frac{z}{4}$时，取等号，
故x2+y2+z2 的最小值为$\frac{1}{21}$，
故选：B．
点评 本题主要考查柯西不等式应用，属于基础题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
18．
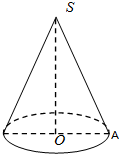如图，课桌上放着一个圆锥SO，点A为圆锥底面圆周上一点，SA=2cm，OA=1cm，蚂蚁从点A沿圆锥的侧面爬行一周再回到A，则蚂蚁行迹的最短路程是（ ）
如图，课桌上放着一个圆锥SO，点A为圆锥底面圆周上一点，SA=2cm，OA=1cm，蚂蚁从点A沿圆锥的侧面爬行一周再回到A，则蚂蚁行迹的最短路程是（ ）| A． | 2πcm | B． | 2$\sqrt{2}$cm | C． | 4$\sqrt{2}$cm | D． | 4cm |
1．经过点M（1，5）且倾斜角为$\frac{2π}{3}$的直线的参数方程是（ ）
| A． | $\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=5+\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{3}}}{2}t}\\{y=5+\frac{1}{2}t}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{3}}}{2}t}\\{y=5-\frac{1}{2}t}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=5-\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$ |