题目内容
18．若2弧度的圆心角所对的弧长为2cm，则这个圆心角所夹的扇形的面积是1cm2．分析 结合弧长公式，求圆的半径，再利用扇形的面积公式，即可得解．
解答 解：弧度是2的圆心角所对的弧长为2，
所以根据弧长公式，可得圆的半径为1，
所以扇形的面积为：$\frac{1}{2}$×2×1=1cm2，
故答案为：1．
点评 本题主要考查了扇形的弧长公式与扇形的面积公式的应用，属于基础题．
练习册系列答案
相关题目
9．设随机变量ξ～B（2，p），η～B（3，p），若P（ξ≥1）=$\frac{5}{9}$，则P（η≥2）的值为（ ）
| A． | $\frac{20}{27}$ | B． | $\frac{8}{27}$ | C． | $\frac{7}{27}$ | D． | $\frac{1}{27}$ |
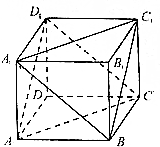已知正方体ABCD-A1B1C1D1的棱长为a．
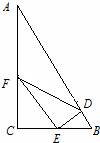某个公园有个池塘，其形状为直角△ABC，∠C=90°，AB=2百米，BC=1百米，现在准备养一批供游客观赏的鱼，分别在AB，BC，CA上取点D，E，F，如图，使得EF∥AB，EF⊥ED，在△DEF喂食，求S△DEF的最大值．
10．若x+2y+4z=1，则x2+y2+z2的最小值是（ ）
| A． | 21 | B． | $\frac{1}{21}$ | C． | 16 | D． | $\frac{1}{16}$ |
8．已知某离散型随机变量X的分布列如表格，则m=$\frac{7}{12}$．
| X | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{4}$ | m |