题目内容
设f(x)=(k+1)x2-(2k+1)x+1,x∈R,若x∈(1,3),f(2x-x)>0恒成立,求k的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:令t=2x-x,可求1<t<5,原命题等价于等价于1<t<5时,f(t)>0恒成立;即(k+1)t2-(2k+1)t+1>0恒成立,再分三种情况讨论二次函数得出结论.
解答:
解:令t=2x-x,
t′=2xln2-1,∵x>1,∴2x>2,∴2xln2-1>2ln2-1=ln
>ln1=0,
∴x∈(1,3)时,t′>0,∴t=2x-x在x∈(1,3)上递增,∴1<t<5,
故x∈(1,3),f(2x-x)>0恒成立,等价于1<t<5时,f(t)>0恒成立;即(k+1)t2-(2k+1)t+1>0恒成立,
当k+1=0时,即k=-1时,不等式变为t+1>0,故1<t<5时,f(t)>0恒成立;∴k=-1满足要求;
当k+1≠0时,令g(t)=(k+1)t2-(2k+1)t+1,对称轴为x=1-
,
①当k+1>0即k>-1时,抛物线开口向上,对称轴x=1-
<1,故函数在(1,5)递增,只要g(1)>0即可,
∴(k+1)-(2k+1)+1>0,∴k<1,
此时k的范围为-1<k<1;
②当k+1<0即k<-1时,抛物线开口向下,对称轴x=1-
>1,又函数恒过(0,1),如图:
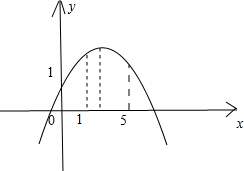
只要g(5)>0,∴(k+1)52-5(2k+1)+1>0,∴k>-
此时k的范围为-
<k<-1;
综上,k的范围为{k|-
<k<1}
t′=2xln2-1,∵x>1,∴2x>2,∴2xln2-1>2ln2-1=ln
| 4 |
| e |
∴x∈(1,3)时,t′>0,∴t=2x-x在x∈(1,3)上递增,∴1<t<5,
故x∈(1,3),f(2x-x)>0恒成立,等价于1<t<5时,f(t)>0恒成立;即(k+1)t2-(2k+1)t+1>0恒成立,
当k+1=0时,即k=-1时,不等式变为t+1>0,故1<t<5时,f(t)>0恒成立;∴k=-1满足要求;
当k+1≠0时,令g(t)=(k+1)t2-(2k+1)t+1,对称轴为x=1-
| 1 |
| 2(k+1) |
①当k+1>0即k>-1时,抛物线开口向上,对称轴x=1-
| 1 |
| 2(k+1) |
∴(k+1)-(2k+1)+1>0,∴k<1,
此时k的范围为-1<k<1;
②当k+1<0即k<-1时,抛物线开口向下,对称轴x=1-
| 1 |
| 2(k+1) |
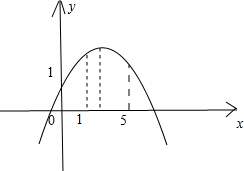
只要g(5)>0,∴(k+1)52-5(2k+1)+1>0,∴k>-
| 7 |
| 5 |
此时k的范围为-
| 7 |
| 5 |
综上,k的范围为{k|-
| 7 |
| 5 |
点评:本题主要考查函数与不等式之间的关系,综合性较强,属于较难的题目.

练习册系列答案
相关题目
下列函数中,在区间[0,
]上为减函数的是( )
| π |
| 2 |
| A、y=sinx | ||
| B、y=cosx | ||
| C、y=tanx | ||
D、y=sin(x-
|
在单位圆上,点P从(0,1)出发,沿单位圆x2+y2=1顺时针方向运动
弧长到达Q点,则Q 点的坐标为( )
| 2π |
| 3 |
A、(-
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(-
|
命题“?x0∈R,2 x0≤0”的否定为( )
| A、?x∈R,2x≤0 |
| B、?x∈R,2x≥0 |
| C、?x∈R,2x<0 |
| D、?x∈R,2x>0 |
如图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
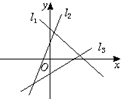

| A、k1<k2<k3 |
| B、k3<k1<k2 |
| C、k3<k2<k1 |
| D、k1<k3<k2 |
用小立方块搭一个几何体,使它的正视图和俯视图如图所示,则它需要的小立方块的个数最多是( )
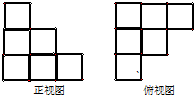

| A、12 | B、13 | C、14 | D、15 |