题目内容
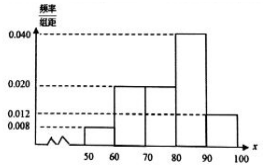
3. 某研究所设计了一款智能机器人,为了检验设计方案中机器人动作完成情况,现委托某工厂生产500个机器人模型,并对生产的机器人进行编号:001,002,…,500,采用系统抽样的方法抽取一个容量为50的机器人样本,试验小组对50个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
某研究所设计了一款智能机器人,为了检验设计方案中机器人动作完成情况,现委托某工厂生产500个机器人模型,并对生产的机器人进行编号:001,002,…,500,采用系统抽样的方法抽取一个容量为50的机器人样本,试验小组对50个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:| 分组 | 机器人数 | 频率 |
| [50,60) | 0.08 | |
| [60,70) | 10 | |
| [70,80) | 10 | |
| [80,90) | ||
| [90,100] | 6 |
(2)若随机抽的第一个号码为003,这500个机器人分别放在A,B,C三个房间,从001到200在A房间,从201到355在B房间,从356到500在C房间,求B房间被抽中的人数是多少?
(3)从动作个数不低于80的机器人中随机选取2个机器人,该2个机器人中动作个数不低于90的机器人记为ξ,求ξ的分布列与数学期望.
分析 (1)根据题意填写频率分布直方图与频率分布表中的部分数据;
(2)根据系统抽样分段间隔相等,计算抽取的样本数据个数;
(3)由题意知ξ的可能取值,计算对应的概率值,
写出ξ的分布列,计算数学期望值.
解答 解:(1)根据题意,50×0.08=4,50-4-10-10-6=20,计算对应的频率,填写频率分布直方图及频率分布表,
| 分组 | 机器人数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 10 | 0.2 |
| [70,80) | 10 | 0.2 |
| [80,90) | 20 | 0.4 |
| [90,100] | 6 | 0.12 |
(2)系统抽样的分段间隔为$\frac{500}{50}=10$,
在随机抽样中,首次抽到003号,以后每隔10个抽到一个,
则被抽中的机器人数构成以3为首项,10为公差的等差数列,
故可分别求出在001到200中有20个,在201至355号中共有16个,
(3)该2个机器人中动作个数不低于90的机器人数记为ξ,
ξ的取值为0,1,2,
所以P(ξ=0)=$\frac{{C}_{20}^{2}}{{C}_{26}^{2}}$=$\frac{38}{65}$,
P(ξ=1)=$\frac{{C}_{20}^{1}{•C}_{6}^{1}}{{C}_{26}^{2}}$=$\frac{24}{65}$,
P(ξ=2)=$\frac{{C}_{6}^{2}}{{C}_{26}^{2}}$=$\frac{3}{65}$;
所以ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{38}{65}$ | $\frac{24}{65}$ | $\frac{3}{65}$ |
点评 本题考查了离散型随机变量的分布列与数学期望问题,也考查了频率分布表与直方图的应用问题,是中档题.

练习册系列答案
相关题目
8.已知单位向量$\overrightarrow a,\overrightarrow b$满足$\overrightarrow a⊥\overrightarrow b$,向量$\overrightarrow m=2\overrightarrow a-\sqrt{t-1}\overrightarrow b,\overrightarrow n=t\overrightarrow a+\overrightarrow b$,(t为正实数),则$\overrightarrow m•\overrightarrow n$的最小值为( )
| A. | $\frac{15}{8}$ | B. | $\frac{5}{2}$ | C. | $\frac{15}{4}$ | D. | 0 |
15.过点(1,-3)且垂直于于直线x-2y+3=0的直线方程为( )
| A. | x-2y-7=0 | B. | 2x+y+1=0 | C. | x-2y+7=0 | D. | 2x+y-1=0 |
13.设α为锐角,sinα=$\frac{3}{5}$,则cosα=( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{16}{25}$ | D. | $-\frac{16}{25}$ |