题目内容
16.不等式|x-4|≤3 的整数解的个数是7.分析 去绝对值求出不等式的解集,从而求出整数解的个数即可.
解答 解:∵|x-4|≤3,
∴-3≤x-4≤3,
∴1≤x≤7,
故不等式的整数解的个数是7个,
故答案为:7.
点评 本题考查了解绝对值不等式问题,是一道基础题.

练习册系列答案
相关题目
6.在区间[1,5]和[2,4]上分别各取一个数,记为m和n,则方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
7.执行如图所示的程序框图,若输出的结果是$\frac{99}{199}$,则判断框内应填的内容是( )


| A. | n≤97 | B. | n≤98 | C. | n≤99 | D. | n≤100 |
1.如图的程序框图,其作用是输入x的值,输出相应的y值,若x=y,则这样的x值有( )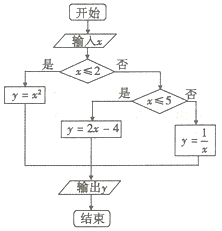

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
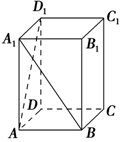 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.
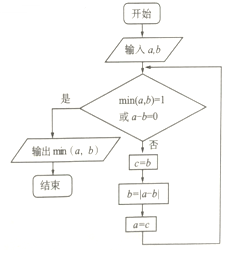 min(a,b)表示中的最小值.执行如图所示的程序框图,若输入的a,b值分别为6,4,则输出的min(a,b)值是( )
min(a,b)表示中的最小值.执行如图所示的程序框图,若输入的a,b值分别为6,4,则输出的min(a,b)值是( )