题目内容
6.过点P(3,2)且在两坐标轴上的截距相等的直线方程是( )| A. | x-y-1=0 | B. | x+y-5=0或2x-3y=0 | ||
| C. | x+y-5=0 | D. | x-y-1=0或2x-3y=0 |
分析 当横截距a=0时,纵截距b=a=0,此时直线方程过点P(3,2)和原点(0,0;当横截距a≠0时,纵截距b=a,此时直线方程为$\frac{x}{a}+\frac{y}{a}=1$.由此能求出结果.
解答 解:当横截距a=0时,纵截距b=a=0,
此时直线方程过点P(3,2)和原点(0,0),
直线方程为:$\frac{y}{x}=\frac{2}{3}$,整理,得2x-3y=0;
当横截距a≠0时,纵截距b=a,
此时直线方程为$\frac{x}{a}+\frac{y}{a}=1$,
把P(3,2)代入,得:$\frac{3}{a}+\frac{2}{a}=1$,解得a=5,
∴直线方程为$\frac{x}{5}+\frac{y}{5}=1$,即x+y-5=0.
∴过点P(3,2)且在两坐标轴上的截距相等的直线方程是x+y-5=0或2x-3y=0.
故选:B.
点评 本题考查直线方程的求法,是基础题,解题时要认真审题,注意两点式方程和截距式方程的性质的合理运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
18.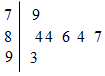 如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
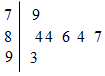 如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85,1.6 | B. | 84,4 | C. | 84,1.6 | D. | 85,4 |
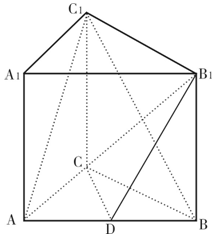 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.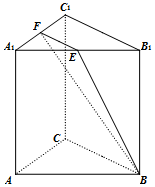 三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.
三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.