题目内容
在极坐标系中，已知直线l过点A（1，0），且其向上的方向与极轴的正方向所成的最小正角为
，求：
（1）直线的极坐标方程；
（2）极点到该直线的距离．
| π |
| 3 |
（1）直线的极坐标方程；
（2）极点到该直线的距离．
考点：简单曲线的极坐标方程
专题：空间位置关系与距离
分析：（1）根据正弦定理，求出直线的极坐标方程即可；
（2）作OH⊥l，垂足为H，在△OHA中，OA=1，∠OHA=
，∠OAH=
，则OH=OAsin
=
，据此解答即可．
（2）作OH⊥l，垂足为H，在△OHA中，OA=1，∠OHA=
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
解答：
解：（1）由正弦定理得
=
，
即ρsin（
-θ）=sin
=
，
∴所求直线的极坐标方程为ρsin（
-θ）=
．
（2）作OH⊥l，垂足为H，在△OHA中，
OA=1，∠OHA=
，∠OAH=
，
则OH=OAsin
=
，
即极点到该直线的距离等于
．
| ρ | ||
sin
|
| 1 | ||
sin(
|
即ρsin（
| π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
∴所求直线的极坐标方程为ρsin（
| π |
| 3 |
| ||
| 2 |
（2）作OH⊥l，垂足为H，在△OHA中，
OA=1，∠OHA=
| π |
| 2 |
| π |
| 3 |
则OH=OAsin
| π |
| 3 |
| ||
| 2 |
即极点到该直线的距离等于
| ||
| 2 |
点评：本题主要考查了求直线的极坐标方程的方法，考查了点线之间的距离，属于基础题．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
相关题目
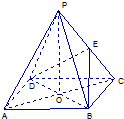如图所示，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，底面边长AB=1，E是PC的中点．