Question

已知函数f(x)＝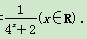

(1)证明：f(x)＋f(1－x)＝；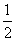

(2)若数列{a_n}的通项公式为a_n＝f(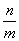)(m∈N^*，n＝1,2，…，m)，求数列{a_n}的前m项和S_m；

(3)设数列{b_n}满足b₁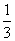＝，b_n＋1＝b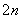＋b_n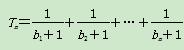，，若(2)中的S_m满足对不小于2的任意正整数m，S_m<T_n恒成立，试求正整数m的最大值．

Answer 1

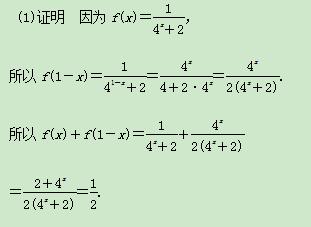(2)解　由(1)，知f(x)＋f(1－x)＝，

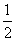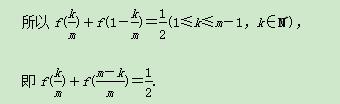所以a_k＋a_m－k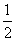＝，a_m＝f(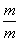)＝f(1)＝.

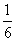又S_m＝a₁＋a₂＋…＋a_m－1＋a_m，①

S_m＝a_m－1＋a_m－2＋…＋a₁＋a_m，②

由①＋②，得2S_m＝(m－1)×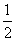＋2a_m＝－，

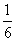即S_m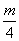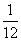＝－(m∈N^*)．

(3)解　由b₁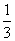＝，b_n＋1＝b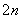＋b_n＝b_n(b_n＋1)，

显然对任意n∈N^*，b_n>0，

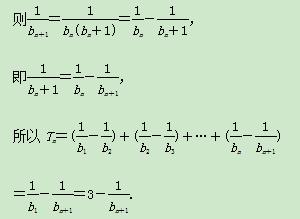因为b_n＋1－b_n＝b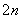>0，

所以b_n＋1>b_n，

即数列{b_n}是单调递增数列．

所以T_n关于n递增，所以当n∈N^*时，T_n≥T₁.

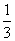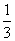因为b₁＝，b₂＝()²＋＝，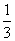

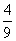所以T_n≥T₁＝3－＝.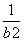

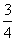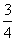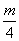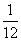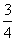由题意，知S_m<，即－<，解得m<，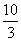

所以正整数m的最大值为3.