题目内容
已知数列{an}满足a1＝1，an＋1＝3an＋1.
(1)证明{an＋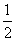
}是等比数列，并求{an}的通项公式；
(2)证明
＋
＋…＋
<
.
证明 (1)由an＋1＝3an＋1
得an＋1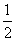＋＝3(an＋)．
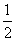又a1＋＝，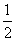
所以{an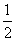＋}是首项为，公比为3的等比数列．
an＋＝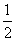
，因此{an}的通项公式为an＝
.
(2)由(1)知＝
.
因为当n≥1时，3n－1≥2×3n－1，
所以
.
于是＋＋…＋≤1＋
＋…＋
＝(1－
)<.
所以＋＋…＋<.
练习册系列答案
阅读快车系列答案
相关题目
和曲线
所围成的图形的面积为________.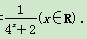
；
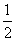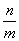)(m∈N*，n＝1,2，…，m)，求数列{an}的前m项和Sm；
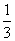，bn＋1＝b
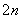＋bn，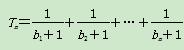
，若(2)中的Sm满足对不小于2的任意正整数m，Sm<Tn恒成立，试求正整数m的最大值．
的展开式中x3项的系数为20，则a2＋b2的最小值为________．
A．
B．
D．
，则
；
的图像与函数
的图像关于
轴对称，且
，则
的取值范围是 ;