题目内容
已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为________.
(0,1)∪(9,+∞)
解析 设y1=f(x)=|x2+3x|,y2=a|x-1|,
在同一直角坐标系中作出y1=|x2+3x|,y2=a|x-1|的图象如图所示.
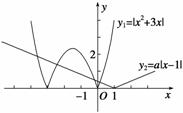
由图可知f(x)-a|x-1|=0有4个互异的实数根等价于y1=|x2+3x|与y2=a|x-1|的图象有4个不同的交点,
当4个交点横坐标都小于1时,
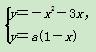 有两组不同解x1,x2,
有两组不同解x1,x2,
消y得x2+(3-a)x+a=0,
故Δ=a2-10a+9>0,
且x1+x2=a-3<2,x1x2=a<1,
联立可得0<a<1.
当4个交点横坐标有两个小于1,两个大于1时,
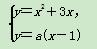 有两组不同解x3,x4.
有两组不同解x3,x4.
消去y得x2+(3-a)x+a=0,
故Δ=a2-10a+9>0,
且x3+x4=a-3>2,x3x4=a>1,
联立可得a>9,

练习册系列答案
相关题目
 ),C(3,0),动点D满足|
),C(3,0),动点D满足|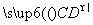 |=1,则|
|=1,则|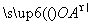 +
+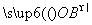 +
+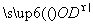 |的取值范围是( )
|的取值范围是( )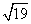 -1,
-1,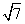 ] D.[
] D.[ 和曲线
和曲线 所围成的图形的面积为________.
所围成的图形的面积为________.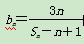 的前n项和为Tn,证明:Tn<6.
的前n项和为Tn,证明:Tn<6.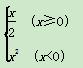 , 则f[f(x)]≥1的充要条件是( )
, 则f[f(x)]≥1的充要条件是( )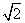 ]
] 的前100项和为( )
的前100项和为( ) B.
B. C.
C. D.
D.
 ;
;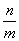 )(m∈N*,n=1,2,…,m),求数列{an}的前m项和Sm;
)(m∈N*,n=1,2,…,m),求数列{an}的前m项和Sm;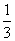 ,bn+1=b
,bn+1=b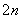 +bn,
+bn,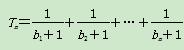 ,若(2)中的Sm满足对不小于2的任意正整数m,Sm<Tn恒成立,试求正整数m的最大值.
,若(2)中的Sm满足对不小于2的任意正整数m,Sm<Tn恒成立,试求正整数m的最大值. ,则
,则 ;
;