题目内容
16.已知直线y=x+2交椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)于A、B两点.(I)求椭圆C的离心率的取值范围;
(Ⅱ)设M为C上区别于A、B的任意一点,且$\overrightarrow{OM}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(O为坐标原点),λ2+μ2=1,求a的值.
分析 (Ⅰ)将直线方程代入椭圆方程,利用判别式大于0,可得a的范围,再由离心率公式,计算即可得到所求范围;
(Ⅱ)运用向量的坐标运算,确定坐标之间的关系,利用M,A,B在椭圆上,结合韦达定理,化简整理,可得a的方程,解方程可得a的值.
解答 解:(Ⅰ)将直线y=x+2代入椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,可得
(1+a2)x2+4a2x+3a2=0,
由△=16a4-4(1+a2)(3a2)>0,
可得a>$\sqrt{3}$或a<-$\sqrt{3}$(舍去),
即有e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-1}}{a}$=$\sqrt{1-\frac{1}{{a}^{2}}}$∈($\frac{\sqrt{6}}{3}$,1);
(Ⅱ)设M(x,y),A(x1,y1),B(x2,y2),
由$\overrightarrow{OM}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,可得
x=λx1+μx2,y=λy1+μy2.
又因为点M在椭圆C上,所以有(λx1+μx2)2+a2(λy1+μy2)2=a2,
整理可得:λ2(x12+a2y12)+μ2(x22+a2y22)+2λμ(x1x2+a2y1y2)=a2.
即为(λ2+μ2)a2+2λμ(x1x2+a2y1y2)=a2.
由λ2+μ2=1,可得x1x2+a2y1y2=0,
又x1+x2=-$\frac{4{a}^{2}}{1+{a}^{2}}$,x1x2=$\frac{3{a}^{2}}{1+{a}^{2}}$,
可得x1x2+a2y1y2=x1x2+a2(x1+2)(x2+2)=0,
即有(1+a2)x1x2+2a2(x1+x2)+4a2=0,
可得(1+a2)•$\frac{3{a}^{2}}{1+{a}^{2}}$+2a2(-$\frac{4{a}^{2}}{1+{a}^{2}}$)+4a2=0,
解得a=$\sqrt{7}$.
点评 本题考查椭圆的方程与性质,考查直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,考查学生的计算能力,属于中档题.

测量产品中的微量元素x,y的含量(单位:微克),当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.已知该天甲厂生产的产品共有98件,如表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(2)用上述样本数据统计乙厂该天生产的优等品的数量;
(3)从乙厂抽取的上述5件产品中,随机抽取2件.求抽取的2件产品中优等品的件数X的分布列及数学期望.
| A. | 252 | B. | -252 | C. | 160 | D. | -160 |
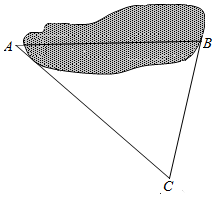 A,B两地之间隔着一个水塘(如图),现选择另一点C,测得CA=10$\sqrt{7}$km,CB=10km,∠CBA=60°.
A,B两地之间隔着一个水塘(如图),现选择另一点C,测得CA=10$\sqrt{7}$km,CB=10km,∠CBA=60°.