题目内容
已知f（x），g（x）都是定义在R上的函数，并满足以下条件：
（1）f（x）=3axg（x），（a＞0，a≠1）；
（2）g（x）≠0；
（3）f（x）g′（x）＜f′（x）g（x）．
若
+
=10，则a=（ ）
（1）f（x）=3axg（x），（a＞0，a≠1）；
（2）g（x）≠0；
（3）f（x）g′（x）＜f′（x）g（x）．
若
| f(-1) |
| g(-1) |
| f(1) |
| g(1) |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
考点：函数的值
专题：导数的概念及应用
分析：先根据
+
=10得到含a的式子，求出a的两个值，再由已知，利用导数判断函数
=3ax的单调性求a的范围，判断a的两个之中哪个成立即可．
| f(-1) |
| g(-1) |
| f(1) |
| g(1) |
| f(x) |
| g(x) |
解答：
解：由
+
=10，得3a+3a-1=10，
所以a=3或a=
．
又由f（x）•g′（x）＜f′（x）•g（x），即f（x）g′（x）-f′（x）g（x）＜0，
也就是(
)′=-
＞0，说明函数
=3ax是增函数，
即a＞1．∴a=3．
故选：B．
| f(-1) |
| g(-1) |
| f(1) |
| g(1) |
所以a=3或a=
| 1 |
| 3 |
又由f（x）•g′（x）＜f′（x）•g（x），即f（x）g′（x）-f′（x）g（x）＜0，
也就是(
| f(x) |
| g(x) |
| f(x)g′(x)-f′(x)g(x) |
| g2(x) |
| f(x) |
| g(x) |
即a＞1．∴a=3．
故选：B．
点评：本题考查了应用导数判断函数的单调性，做题时应认真观察．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
（理科）
tan21°tan39°-tan159°+tan39°=（ ）
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知命题p：?x∈R，2x＜3x；命题q：?x∈R，2x≥1+x2，则命题p，q的真假是（ ）
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
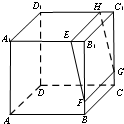如图，平面EFGH为长方体ABCD-A1B1C1D1的截面，E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，EH∥A1D1，则四边形EFGH的形状是（ ）| A、平行四边形 | B、梯形 |
| C、菱形 | D、矩形 |
由①y=2x+5是一次函数；②y=2x+5的图象是一条直线；③一次函数的图象是一条直线．写一个“三段论”形式的正确推理，则作为大前提、小前提和结论的分别是（ ）
| A、②①③ | B、③①② |
| C、①②③ | D、②③① |
已知点P是抛物线y2=4x上一点，设点P到直线x=-1的距离为d1，到直线x+2y+10=0的距离为d2，则d1+d2的最小值是（ ）
| A、5 | ||||
| B、4 | ||||
C、
| ||||
D、
|