题目内容
在数列{an}中，已知a1=2，a2=7，记an与an+1（n∈N+）的积的个位数为an+2，则a2015= ．
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：由已知分别求出数列的前几项，然后得到数列周期性出现的规律得答案．
解答：
解：∵a1=2，a2=7，∴a1a2=14，则a3=4，
a2a3=7×4=28，则a4=8，
a3a4=4×8=32，则a5=2，
a4a5=8×2=16，则a6=6．
∴a7=2，a8=2，a9=4，a10=8，a11=2，
∴从第三项起，an的值成周期数列，周期数为6，
则a2015=a335×6+5=a5=2．
故答案为：2．
a2a3=7×4=28，则a4=8，
a3a4=4×8=32，则a5=2，
a4a5=8×2=16，则a6=6．
∴a7=2，a8=2，a9=4，a10=8，a11=2，
∴从第三项起，an的值成周期数列，周期数为6，
则a2015=a335×6+5=a5=2．
故答案为：2．
点评：本题考查了数列递推式，关键在于通过求值得到数列的周期性，是中档题．
练习册系列答案
相关题目
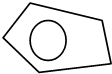如图，在一个不规则多边形内随机撒入200粒芝麻（芝麻落到任何位置的可能性相等），恰有40粒落入半径为1的圆内，则该多边形的面积约为（ ）| A、4π | B、5π | C、6π | D、7π |
