题目内容
10.(1)计算$\frac{2{A}_{8}^{5}+7{A}_{8}^{4}}{{A}_{8}^{8}-{A}_{9}^{5}}$(2)求证:A${\;}_{n+1}^{m}$=mA${\;}_{n}^{m-1}$+A${\;}_{n}^{m}$.
分析 (1)根据排列数的公式进行化简、计算即可;
(2)利用排列数的公式进行证明即可.
解答 解:(1)$\frac{2{A}_{8}^{5}+7{A}_{8}^{4}}{{A}_{8}^{8}-{A}_{9}^{5}}$=$\frac{2×8×7×6×5×4+7×8×7×6×5}{8×7×6×5×4×3×2×1-9×8×7×6×5}$
=$\frac{2×4-7}{4×3×2×1-9}$
=$\frac{1}{15}$;
(2)证明:∵A${\;}_{n+1}^{m}$=$\frac{(n+1)!}{(n-m+1)!}$,
mA${\;}_{n}^{m-1}$+A${\;}_{n}^{m}$=$\frac{m•n!}{(n-m+1)!}$+$\frac{n!}{(n-m)!}$
=$\frac{m•n!+(n-m+1)•n!}{(n-m+1)!}$
=$\frac{(n+1)!}{(n-m+1)!}$,
∴${A}_{n+1}^{m}$=m${A}_{n}^{m-1}$+${A}_{n}^{m}$.
点评 本题考查了排列数公式的应用问题,也考查了计算能力与逻辑推论能力的应用问题,是基础题目.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
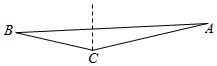 如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.
如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.