题目内容
5.已知数列{an}•{bn}满足a1=2,an-1=an(an+1-1),bn=an-1.(I)求数列{bn}的通项公式;
(Ⅱ)求数列{$\frac{{2}^{n}}{{b}_{n}}$}的前n项和Sn.
分析 (I)an-1=an(an+1-1),bn=an-1.可得:bn=(bn+1)bn+1,化为:$\frac{1}{{b}_{n+1}}$-$\frac{1}{{b}_{n}}$=1.再利用等差数列的通项公式即可得出.
(II)$\frac{{2}^{n}}{{b}_{n}}$=n•2n,利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(I)∵an-1=an(an+1-1),bn=an-1.
∴bn=(bn+1)bn+1,化为:$\frac{1}{{b}_{n+1}}$-$\frac{1}{{b}_{n}}$=1.
∴数列$\{\frac{1}{{b}_{n}}\}$是等差数列,首项为1,公差为1.
∴$\frac{1}{{b}_{n}}$=1+(n-1)=n,
可得bn=$\frac{1}{n}$.
(II)$\frac{{2}^{n}}{{b}_{n}}$=n•2n.
∴数列{$\frac{{2}^{n}}{{b}_{n}}$}的前n项和Sn=2+2×22+3×23+…+n×2n,
2Sn=22+2×23+…+(n-1)×2n+n×2n+1,
∴-Sn=2+22+…+2n-n×2n+1=$\frac{2×({2}^{n}-1)}{2-1}$-n×2n+1=(1-n)×2n+1-2,
∴Sn=(n-1)×2n+1+2.
点评 本题考查了递推关系、“错位相减法”、等比数列的通项公式与前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.设x>0,y>0,下列各式中正确的是( )
| A. | ln(x+y)=lnx+lny | B. | $\frac{lgx}{lgy}$=lg$\frac{x}{y}$ | C. | lg$\frac{x}{y}$=lgx-lgy | D. | lg(xy)=lgx•lgy |
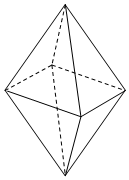 已知四面体的6条棱所在的直线中有3对异面直线,那么在过正八面体(由2个棱长相同的四棱锥拼接而成,如图所示)的任意2个顶点的所有直线中,随机取2条,则这2条直线异面的情况有24种.
已知四面体的6条棱所在的直线中有3对异面直线,那么在过正八面体(由2个棱长相同的四棱锥拼接而成,如图所示)的任意2个顶点的所有直线中,随机取2条,则这2条直线异面的情况有24种.