题目内容
(1)函数y=x2+x+2的递增区间是 ;
(2)y=-x2-4mx+1在[2,+∞)上是减函数,则m取值范围是 .
(2)y=-x2-4mx+1在[2,+∞)上是减函数,则m取值范围是
考点:函数的单调性及单调区间
专题:函数的性质及应用
分析:(1)求改函数的对称轴,即可得到该函数的单调递增区间;
(2)该函数的对称轴是x=-2m,因为该函数在[2,+∞)上是减函数,所以-2m≤2,m≥-1.
(2)该函数的对称轴是x=-2m,因为该函数在[2,+∞)上是减函数,所以-2m≤2,m≥-1.
解答:
解:(1)y=x2+x+2,对称轴为x=-
;
∴该函数的递增区间是(-
,+∞);
(2)y=-x2-4mx+1,对称轴为x=-2m,该函数在[2,+∞)上是减函数;
∴-2m≤2,m≥-1;
m取值范围是[-1,+∞).
故答案为:(-
,+∞),[-1,+∞).
| 1 |
| 2 |
∴该函数的递增区间是(-
| 1 |
| 2 |
(2)y=-x2-4mx+1,对称轴为x=-2m,该函数在[2,+∞)上是减函数;
∴-2m≤2,m≥-1;
m取值范围是[-1,+∞).
故答案为:(-
| 1 |
| 2 |
点评:考查二次函数的单调性和对称轴的关系:在对称轴的一边具有单调性.

练习册系列答案
相关题目
函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x.若在区间[-2,2]上方程ax+a-f(x)=0恰有三个不相等的实数根,则实数a的取值范围是( )
| A、[0,1) |
| B、[0,2] |
| C、[1,+∞) |
| D、[2,+∞) |
下列各组中的两个函数是同一函数的为( )
(1)y=
,y=x-5;
(2)y=
,y=
;
(3)y=|x|,y=
;
(4)y=x,y=
;
(5)y=(2x-5)2,y=|2x-5|.
(1)y=
| (x+3)(x-5) |
| x+3 |
(2)y=
| x+1 |
| x-1 |
| (x+1)(x-1) |
(3)y=|x|,y=
| x2 |
(4)y=x,y=
| 3 | x3 |
(5)y=(2x-5)2,y=|2x-5|.
| A、(1),(2) |
| B、(2),(3) |
| C、(3),(5) |
| D、(3),(4) |
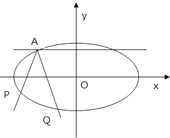 如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).
如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).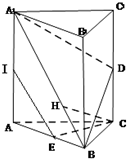 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.