题目内容
7．若$\overrightarrow a=（-3，2，5），\overrightarrow b=（1，-3，0），\overrightarrow c=（7，-2，1）$，则$（\overrightarrow a+\overrightarrow b）•\overrightarrow c$=-7．分析 利用空间向量的加法和数量积的坐标运算公式运算即可．
解答 解：$\overrightarrow a=（-3，2，5），\overrightarrow b=（1，-3，0），\overrightarrow c=（7，-2，1）$，则$（\overrightarrow a+\overrightarrow b）•\overrightarrow c$=（-2，-1，5）•（7，-2，1）=-14+2+5=-7；
故答案为：-7．
点评 本题考查了空间向量的加法和数量积运算；属于基础题．
练习册系列答案
相关题目
17．函数f（x）=ax2+2（a-3）x+1在区间[-2，+∞）上递减，则实数a的取值范围是（ ）
| A． | （-∞，0） | B． | [-3，+∞） | C． | [-3，0] | D． | （0，+∞） |
12．
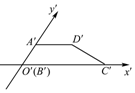已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是（ ）
已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是（ ）| A． | $\sqrt{5}$ | B． | $2\sqrt{2}$ | C． | $2\sqrt{5}$ | D． | $\sqrt{3}$ |
19．“a3＞b3”是“a＞b”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
中，
的对边分别为
，且
的大小
求
的值商丘市某高中从参加高三年级期中考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），数学成绩分组及各组频数如下：
[40,50），2；[50,60），3；[60,70），14；[70,80），15；[80,90），12；[90,100），4．
（Ⅰ）请把给出的样本频率分布表中的空格都填上；
（Ⅱ）估计成绩在85分以上学生的比例；
（Ⅲ）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩[90,100）中选两位同学，共同帮助成绩在[40,50）中的某一位同学．已知甲同学的成绩为42分，乙同学的成绩为95分，求甲、乙两同学恰好被安排在同一小组的概率．
样本频率分布表
分组 | 频数 | 频率 |
[40,50） | 2 | 0．04 |
[50,60） | 3 | 0．06 |
[60,70） | 14 | 0．28 |
[70,80） | 15 | 0．30 |
[80,90） | ||
[90,100） | 4 | 0．08 |
合计 |