题目内容
2.设定义在[-2,2]上的偶函数f(x)在区间[-2,0]上单调递减,若f(1-m)<f(1+m),求实数m的取值范围.分析 根据题意,由函数的奇偶性与单调性分析可得f(x)在[-2,0]上单调递减,进而分析可得$\left\{\begin{array}{l}-2≤1-m≤2①\\-2≤1+m≤2②\\|{1-m}|<|{1+m}|③\end{array}\right.$,解可得m的取值范围,即可得答案.
解答 解:∵f(x)是[-2,2]上的偶函数,
且在[-2,0]上单调递减,
∴f(x)在[0,2]上单调递增,
由f(1-m)<f(1+m)得$\left\{\begin{array}{l}-2≤1-m≤2①\\-2≤1+m≤2②\\|{1-m}|<|{1+m}|③\end{array}\right.$
解①得-3≤m≤1,
解②得-1≤m≤3,
由①②得-1≤m≤1,
则③可化简为(1-m)2<(1+m)2,
得m>0,
综上得m的范围为0<m≤1.
点评 本题考查函数的奇偶性与单调性的综合应用,关键是综合利用函数的奇偶性与单调性,得到关于m的不等式组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.如果点P(sinθ,cosθ)位于第四象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.已知抛物线的参数方程为$\left\{{\begin{array}{l}{x=4{t^2}}\\{y=4t}\end{array}}\right.$,若斜率为1的直线经过抛物线的焦点,且与抛物线相交于A,B两点,则线段AB的长为( )
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 8 | D. | 4 |
17.由于电子技术的飞速发展,计算机的成本不断降低,若每隔5年计算机的价格降低$\frac{1}{3}$,现在价格为8100元的计算机经过15年的价格应降为( )
| A. | 2300元 | B. | 2800元 | C. | 2400元 | D. | 2000元 |
11.近几年网购兴起,快递行业迅速发展,某城市A,B两个区域共有150名快递员,为调查他们的送件数量,通过分层抽样获得了部分快递员一天的送件数量,数据如下表(单位:件):
(Ⅰ)估计A区域的快递员人数;
(Ⅱ)在表格中,从A,B区域各随机抽取一人分别记为甲、乙.假设所有快递员送件数量相互独立,求甲的送件数量比乙的送件数量多的概率;
(Ⅲ)表格中A区域数据的标准差记为SA,B区域数据的标准差记为SB,试判断SA和SB的大小(结论不要求证明).
| A区域 | 86 91 95 100 103 112 123 |
| B区域 | 84 92 93 95 95 97 98 106 |
(Ⅱ)在表格中,从A,B区域各随机抽取一人分别记为甲、乙.假设所有快递员送件数量相互独立,求甲的送件数量比乙的送件数量多的概率;
(Ⅲ)表格中A区域数据的标准差记为SA,B区域数据的标准差记为SB,试判断SA和SB的大小(结论不要求证明).
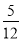 B.
B. C.
C.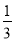 D.
D.