题目内容
18.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,1),则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=5.分析 利用平面向量坐标运算法则先求出$2\overrightarrow{a}+\overrightarrow{b}$,由此能求出结果.
解答 解:∵向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,1),
∴$2\overrightarrow{a}+\overrightarrow{b}$=(0,5),
∴|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{0}^{2}+{5}^{2}}$=5.
故答案为:5.
点评 本题考查向量的模的求法,是基础题,解题时要认真审题,注意平面向量坐标运算法则的合理运用.

练习册系列答案
相关题目
13.如果点P(sinθ,cosθ)位于第四象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.已知抛物线的参数方程为$\left\{{\begin{array}{l}{x=4{t^2}}\\{y=4t}\end{array}}\right.$,若斜率为1的直线经过抛物线的焦点,且与抛物线相交于A,B两点,则线段AB的长为( )
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 8 | D. | 4 |
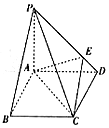 如图,点P是边长为1的正方形ABCD所在平面外一点,PA⊥CD,PA=1,PD=$\sqrt{2}$,E为PD上一点,PE=2ED.
如图,点P是边长为1的正方形ABCD所在平面外一点,PA⊥CD,PA=1,PD=$\sqrt{2}$,E为PD上一点,PE=2ED.
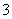 B.
B. C.
C.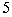 D.
D.