题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2b-c)cos A-acos C=0.
(1)求角A的大小;
(2)若a=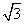 ,S△ABC=
,S△ABC=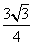 ,试判断△ABC的形状,并说明理由.
,试判断△ABC的形状,并说明理由.
解:(1)法一:由(2b-c)cos A-acos C=0及正弦定理,得
(2sin B-sin C)cos A-sin Acos C=0,
∴2sin Bcos A-sin(A+C)=0,
sin B(2cos A-1)=0.
∵0<B<π,∴sin B≠0,∴cos A=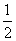 .
.
∵0<A<π,∴A= .
.
法二:由(2b-c)cos A-acos C=0,
及余弦定理,得(2b-c)· =0,整理,得b2+c2-a2=bc,
=0,整理,得b2+c2-a2=bc,
∴cos A= =
=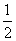 ,
,
∵0<A<π,∴A= .
.
(2)△ABC为等边三角形.
∵S△ABC=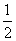 bcsin A=
bcsin A=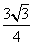 ,
,
即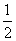 bcsin
bcsin =
=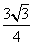 ,
,
∴bc=3,①
∵a2=b2+c2-2bccos A,a=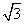 ,A=
,A= ,
,
∴b2+c2=6,②
由①②得b=c=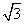 ,
,
∴△ABC为等边三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 -4
-4 D.f(x)=x2+2x
D.f(x)=x2+2x A.
A.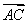 =
=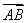 +
+
 =
=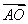 =
=
 =
=
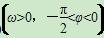 的最小正周期为π,且其图像经过点
的最小正周期为π,且其图像经过点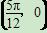 .
.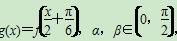 ,且g(α)=1,g(β)=
,且g(α)=1,g(β)=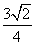 ,求g(α-β)的值.
,求g(α-β)的值. ,则
,则 的值为________.
的值为________.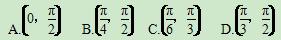
 米,树上另一点B离地面
米,树上另一点B离地面 米,某人在离地面
米,某人在离地面 米的C处看此树,则该人离此树________米时,看A,B的视角最大.
米的C处看此树,则该人离此树________米时,看A,B的视角最大.
 ·
· 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
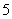 ,矩形
,矩形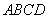 中,
中,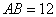 ,
,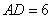 ,
,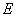 、
、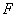 分别为
分别为 、
、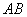 边上的点,且
边上的点,且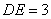 ,
,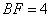 ,将
,将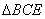 沿
沿 折起至
折起至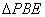 位置(如图
位置(如图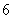 所示),连结
所示),连结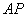 、
、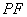 ,其中
,其中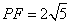 .
.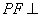 平面
平面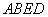 ;
; 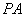 上是否存在点
上是否存在点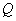 使得
使得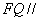 平面
平面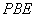 ?若存在,求出点
?若存在,求出点 到平面
到平面