题目内容
6.已知正项等差数列{an}满足a2+a4+a6=9,则log3(a1+$\frac{1}{2}{a}_{3}$+$\frac{1}{2}{a}_{5}$+a7)=2.分析 利用等差数列的通项公式及其性质即可得出.
解答 解:设正项等差数列{an}的公差为d,∵a2+a4+a6=9,
∴3a4=9,解得a4=3.
∴a1+$\frac{1}{2}{a}_{3}$+$\frac{1}{2}{a}_{5}$+a7=a1+$\frac{1}{2}({a}_{3}+{a}_{5})$+a7=3a4=9.
则log3(a1+$\frac{1}{2}{a}_{3}$+$\frac{1}{2}{a}_{5}$+a7)=log39=2.
故答案为:2.
点评 本题考查了等差数列的通项公式及其性质、对数的运算性质,考查了推理能力与计算能力,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.直线y=2x与y=2x+1的位置关系是( )
| A. | 相交但不垂直 | B. | 平行 | C. | 垂直 | D. | 重合 |
11.已知不等式x2+px+q<0的解集是-3<x<2,则( )
| A. | p=-1,q=6 | B. | p=1,q=6 | C. | p=-1,q=-6 | D. | p=1,q=-6 |
18.若点P(2,1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程为( )
| A. | x+y-3=0 | B. | 2x-y-5=0 | C. | 2x+y=0 | D. | x-y-1=0 |
15.关于空间直角坐标系,下列叙述正确的是( )
| A. | P(x,y,z)中x,y,z的位置可以互换的 | |
| B. | 空间直角坐标系中的点与一个三元有序数组是一种一一对应关系 | |
| C. | 空间直角坐标系中的三条坐标轴把空间分成八个部分 | |
| D. | 某点在不同空间直角坐标系中的坐标位置可以相同 |
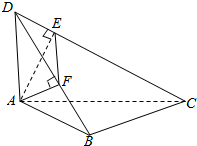 如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.
如图,在空间四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.